Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Construct a DFA recognizing the language {x | the number of 1's is divisible by 2, and 0'sby 3} over an alphabet ā={0,1}
Problem
The given language L={ x | the number of 1's is divisible by 2, and 0's by 3} over an alphabet ∑={0,1}.
Solution
The language is divided into two parts, first we need to find the number of 1’s divisible by 2 and second find out the number of 0’s divisible by 3, finally combine the two parts to generate a result.
Step 1 − DFA for the first part, number of 1’s divisible by 2.
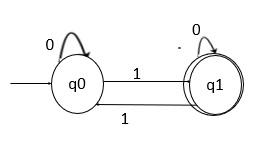
Here,
q0 on 0 goes to q0 which is a final state, and generates a string 0, accepted by the given language.
q0 on 1 goes to q1, q1 on 1 goes to q0 reaches the final state and generates a string “11” which is divisible by 2.
q0 on 0 goes to q0, q0 on 1 goes to q1, q1 on 0 goes to q1 and q1 on 1goes to q0 which is a final state and generates a string “0101”, which is divisible by 2.
Step 2 − DFA for the second part, number of 0’s divisible by 3.
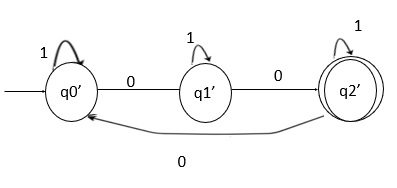
Here,
qo’ on 1 goes to q0 which is a final state and generates a string 1, accepted by the language.
q0’ on 0 goes to q1’, q1’ on o goes to q2’ and q2’ on 0 goes to q0’ which is a final state and generates a string “000” which is divisible by 3.
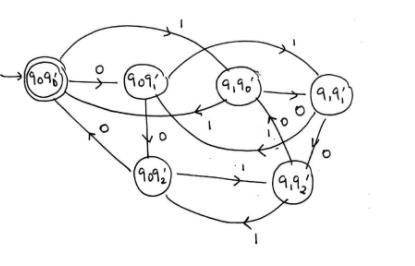
Step 3 − The final DFA is: DFA first part X DFA second part.
| States | 0 | 1 |
|---|---|---|
| {q0q0’} | {q0q1’} | {q1q0’} |
| {q0q1’} | {q0q2’} | {q1q1’} |
| {q0q2’} | {q0q0’} | {q1q2’} |
| {q1q0’} | {q1q1’} | {q0q0’} |
| {q1q1’} | {q1q2’} | {q0q1’} |
| {q1q2’} | {q1q0’} | {q0q2’} |
Transition diagram
The transition diagram for the DFA is as follows −
3K+ Views
