Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Construct DFA for strings not ending with "THE"
A Deterministic Finite automaton (DFA) is a five tuples
M=(Q, Σ, δ,q0,F)
Where,
- Q : Finite set called states.
- Σ : Finite set called alphabets.
- δ : Q × Σ → Q is the transition function.
- q0 ϵ Q is the start or initial state.
- F : Final or accept state.
Accept Strings which are not ending with "THE"
Observe whether the given string is ending with “the” or not.
The different notations of “the” which are avoided in the end of the string are as follows −
"tHE", "thE", "THE", "ThE", "THe", "The", "tHe" and "the"
These all strings are not accepted from alphabet (A-Z)
Let the initial state is q0
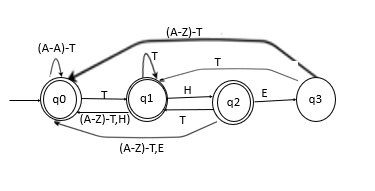
Consider 4 states q0, q1, q2 and q3.
Let’s take a variable named DFA which will be initially 0.
Whenever a transition is there, it will update the value of DFA with the number associated with the new state.
Example
If a transition occurs from state q0 to state q1 then the value of DFA will be updated to 1.
If a transition occurs from state q2 to state q3 then the value of DFA will be updated to 3.
In this way, apply this algorithm on the entire string and if it reaches the end, then reach state 0, 1 or 2. Thus, our string will be accepted. Otherwise, it won’t be accepted.
Case 1
Input − pQdfGTthe
Output − Not Accepted
Case 2
Input − ThesdGTYid
Output − ACCEPTED
577 Views
