Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Construct DFA of a string in which the second symbol from RHS is ‘a’
A Deterministic Finite automaton (DFA) is a 5-tuples
M=(Q, Σ, δ,q0,F)
Where,
- Q : Finite set called states.
- Σ : Finite set called alphabets.
- δ : Q × Σ → Q is the transition function.
- q0 ϵ Q is the start or initial state.
- F : Final or accept state.
Problem
Design a finite automaton where the second symbol from the right hand side is ‘a’.
Solution
The language for a given string over an alphabet {a,b} is −
L={aa,abaa,abbab,aaabab,………}
Example
Input − aaba
Output − Not accepted
Because the second letter from right hand side is not a
Input − aabbab
Output − Accepted
It is complicated to directly construct the DFA.
So, first try to design the non-deterministic finite automata (NFA) and then convert it to the deterministic finite automata (DFA).
Now construct the NFA of the language containing all the strings where the 2nd symbol from the RHS is “a” is given below −
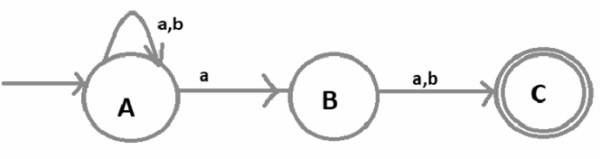
Here,
- A is the initial state.
- B is the intermediate state and
- C is the final state.
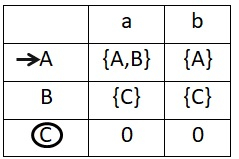
Construct NFA transition table. With the help of a transition table, it is easy to convert the DFA transition table from there to a DFA transition diagram.
The NFA transition table is as follows −
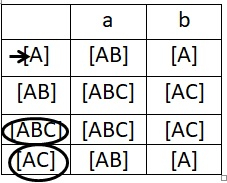
Now convert this NFA transition table to DFA transition table.
We can do this by using the subset configuration on the state transition table of NFA.
The DFA transition table is as follows −
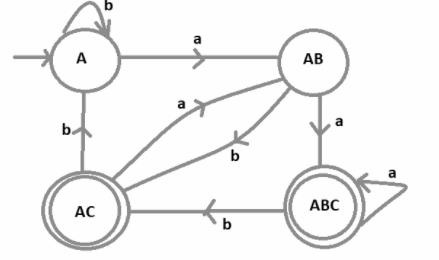
Now, it is comparatively easy to draw the DFA with the help of its transition table.
In this DFA, there are four different states A, AB, ABC and AC, where ABC and AC are the final states because c is the final state in NFA, wherever C is present that state becomes the final state and A is the initial state of the DFA.
2K+ Views
