Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Connectivity of Graph
Whether it is possible to traverse a graph from one vertex to another is determined by how a graph is connected. Connectivity is a basic concept in Graph Theory. Connectivity defines whether a graph is connected or disconnected. It has subtopics based on edge and vertex, known as edge connectivity and vertex connectivity. Let us discuss them in detail.
Connectivity
A graph is said to be connected if there is a path between every pair of vertex. From every vertex to any other vertex, there should be some path to traverse. That is called the connectivity of a graph. A graph with multiple disconnected vertices and edges is said to be disconnected.
Example 1
In the following graph, it is possible to travel from one vertex to any other vertex. For example, one can traverse from vertex 'a' to vertex 'e' using the path 'a-b-e'.
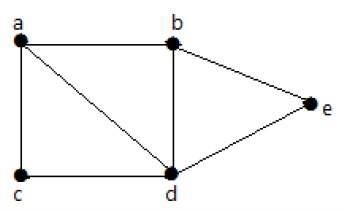
Example 2
In the following example, traversing from vertex 'a' to vertex 'f' is not possible because there is no path between them directly or indirectly. Hence it is a disconnected graph.
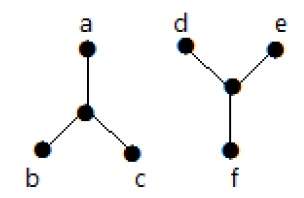
Connectivity Types
Graph Connectivity can be classified broadly into two categories −
Edge Connectivity
Vertex Connectivity
Edge Connectivity
Let 'G' be a connected graph. The minimum number of edges whose removal makes 'G' disconnected is called edge connectivity of G.
Notation − λ(G)
In other words, the number of edges in a smallest cut set of G is called the edge connectivity of G.
If 'G' has a cut edge, then λ(G) is 1. (edge connectivity of G.)
Example
Take a look at the following graph. By removing two minimum edges, the connected graph becomes disconnected. Hence, its edge connectivity (λ(G)) is 2.
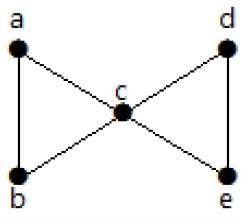
Here are the four ways to disconnect the graph by removing two edges −
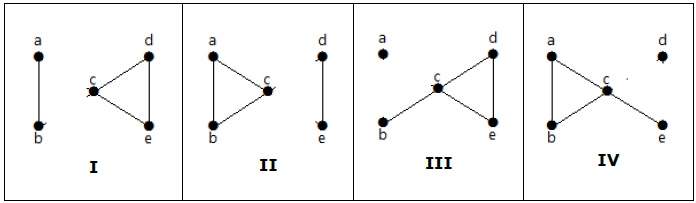
Vertex Connectivity
Let 'G' be a connected graph. The minimum number of vertices whose removal makes 'G' either disconnected or reduces 'G' in to a trivial graph is called its vertex connectivity.
Notation − K(G)
Example
In the above graph, removing the vertices 'e' and 'i' makes the graph disconnected.
If G has a cut vertex, then K(G) = 1.
Notation − For any connected graph G,
K(G) ≤ λ(G) ≤ δ(G)
Vertex connectivity (K(G)), edge connectivity (λ(G)), minimum number of degrees of G(δ(G)).
Example
Calculate λ(G) and K(G) for the following graph −
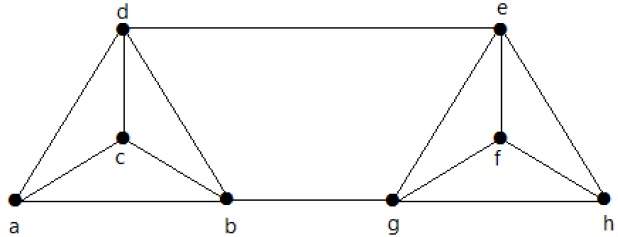
Solution
From the graph,
δ(G) = 3
K(G) ≤ λ(G) ≤ δ(G) = 3 (1)
K(G) ≥ 2 (2)
Deleting the edges {d, e} and {b, h}, we can disconnect G.
Therefore,
λ(G) = 2
2 ≤ λ(G) ≤ δ(G) = 2 (3)
From (2) and (3), vertex connectivity K(G) = 2
291 Views
