
 Data Structure
Data Structure Networking
Networking RDBMS
RDBMS Operating System
Operating System Java
Java MS Excel
MS Excel iOS
iOS HTML
HTML CSS
CSS Android
Android Python
Python C Programming
C Programming C++
C++ C#
C# MongoDB
MongoDB MySQL
MySQL Javascript
Javascript PHP
PHP
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
C++ Program to Check the Connectivity of Undirected Graph Using DFS
The Depth-First Search (DFS) is a graph traversal algorithm that starts at root node and explores as far as possible along each branch before moving to next branch. In this article, we will discuss how to check the connectivity of a graph using DFS traversal algorithm.
Understanding Connectivity of a Graph
A graph is said to be connected if there is a path between every pair of vertices. To check connectivity of a graph, we will try to traverse all nodes using any traversal algorithm. After completing the traversal, if there is any node, which is not visited, then the graph is not connected. To check this using DFS traversal,
- Start DFS traversal from any node (say node 0).
- Track visited vertices using a visited[] array.
- After DFS, if all vertices are visited, the graph is connected. And, if any vertex remains unvisited, the graph is disconnected.
Connected Graph Example
The image below shows an example of a connected graph.
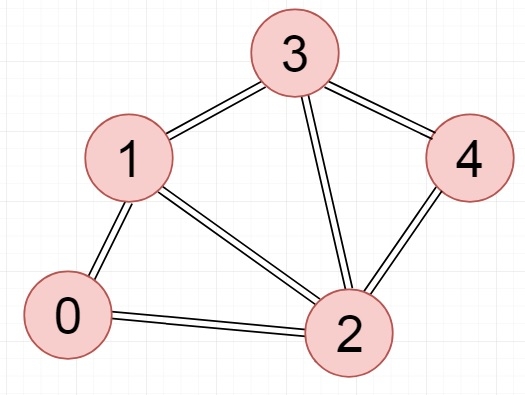
Algorithm to Check Connectivity of a Graph Using DFS
- Step 1: Start
- Step 2: Input the number of vertices V and number of edges E
- Step 3: Create an adjacency list for the graph
- Step 4: For each edge, input the pair of vertices (u, v) and add them to each other's adjacency list
- Step 5: Initialize a visited array of size V with all values set to false
- Step 6: Perform DFS traversal starting from vertex 0
- Step 7: In DFS, for each unvisited adjacent vertex, mark it as visited and call DFS recursively
- Step 8: After DFS, check if all vertices are visited
- Step 9: If all are visited, the graph is connected; otherwise, it's disconnected
- Step 10: End
C++ Program to check Connectivity of a Graph Using DFS
The following C++ program demonstrates how to check the connectivity of a graph using DFS. The program allows the user to input the number of vertices and edges, and then it displays whether the graph is connected or not.
#include <iostream>
#include <vector>
using namespace std;
// Function to perform DFS traversal
void DFS(int v, vector<int> adj[], vector<bool>& visited) {
visited[v] = true;
for (int u : adj[v]) {
if (!visited[u]) {
DFS(u, adj, visited);
}
}
}
// Function to add an undirected edge
void addEdge(vector<int> adj[], int u, int v) {
adj[u].push_back(v);
adj[v].push_back(u);
}
// Function to check connectivity
bool isConnected(vector<int> adj[], int V) {
vector<bool> visited(V, false);
DFS(0, adj, visited);
for (bool v : visited) {
if (!v) return false;
}
return true;
}
int main() {
int V, E;
cout << "Enter number of vertices: ";
cin >> V;
cout << "Enter number of edges: ";
cin >> E;
vector<int> adj[V];
cout << "Enter undirected edges (u v):\n";
for (int i = 0; i < E; ++i) {
int u, v;
cin >> u >> v;
addEdge(adj, u, v);
}
if (isConnected(adj, V))
cout << "The graph is connected.\n";
else
cout << "The graph is disconnected.\n";
return 0;
}
Sample Input
Enter number of vertices: 5 Enter number of edges: 4 Enter undirected edges (u v): 0 1 1 2 2 3 3 4
Sample Output
The graph is connected.

