Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Complement of Graph
Let 'G−' be a simple graph with some vertices as that of 'G' and an edge {U, V} is present in 'G−', if the edge is not present in G. It means, two vertices are adjacent in 'G−' if the two vertices are not adjacent in G.
If the edges that exist in graph I are absent in another graph II, and if both graph I and graph II are combined together to form a complete graph, then graph I and graph II are called complements of each other.
Example
In the following example, graph-I has two edges 'cd' and 'bd'. Its complement graph-II has four edges.
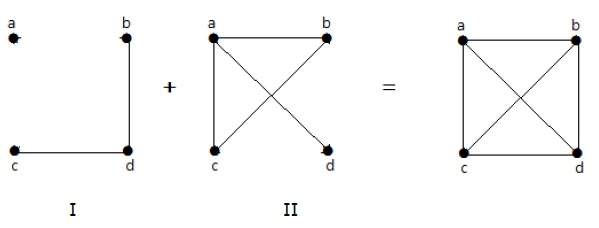
Note that the edges in graph-I are not present in graph-II and vice versa. Hence, the combination of both the graphs gives a complete graph of 'n' vertices.
Note − A combination of two complementary graphs gives a complete graph.
If 'G' is any simple graph, then
|E(G)| + |E('G-')| = |E(Kn)|, where n = number of vertices in the graph.
Example
Let 'G' be a simple graph with nine vertices and twelve edges, find the number of edges in 'G-'.
You have, |E(G)| + |E('G-')| = |E(Kn)|
12 + |E('G-')| =
9(9-1)2 = 9C2
12 + |E('G-')| = 36
|E('G-')| = 24
'G' is a simple graph with 40 edges and its complement 'G−' has 38 edges. Find the number of vertices in the graph G or 'G−'.
Let the number of vertices in the graph be 'n'.
We have, |E(G)| + |E('G-')| = |E(Kn)|
40 + 38 = n(n-1) 2
156 = n(n-1)
13(12) = n(n-1)
n = 13
2K+ Views
