Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Connectivity, Distance, and Spanning Trees
Spanning Tree
One simple definition is that a tree is a connected graph associated with no cycles, where a cycle let's us go from a node to itself without repeating an edge.
A spanning tree for a connected graph G is defined as a tree containing all the vertices of G.
Spanning trees are often implemented for Internet routing Algorithms. In the Internet, computers (nodes) are often connected with many redundant physical connections.
Total number of Spanning Trees in a Graph. If a graph is a complete graph with n no. of vertices, then total number of spanning trees is n(n-2)
where n is denoted as the number of nodes in the graph. In complete graph, the task is equal to counting different labelled trees with n nodes for which have Cayley's formula.
Connectivity
In mathematics and computer science, connectivity is one of the basic concepts of graph theory
it requires the minimum number of elements (nodes or edges) that required to be removed to separate the remaining nodes into isolated subgraphs.
It is closely related to the theory of network flow problems.
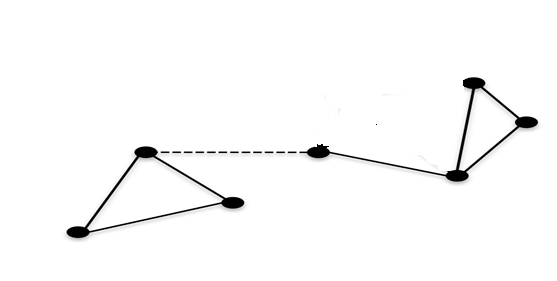
This graph becomes disconnected when the dashed edge is eliminated.
Vertex Connectivity. The vertex connectivity of a graph is the at least number of nodes whose deletion disconnects it.
Vertex connectivity is sometimes denoted as "point connectivity" or simply "connectivity."
Edge Connectivity. The at least number of edges whose deletion from a graph disconnects, also denoted as the line connectivity.
The edge connectivity of a disconnected graph is 0, while that of a connected graph associated with a graph bridge is 1.
Distance
The distance between two nodes can be calculated in terms of lowest common ancestor. Following is the formula.
Dist(d1, d2) = Dist(root, d1) + Dist(root, d2) - 2*Dist(root, lca) 'd1' and 'd2' are the two given keys 'root' is root of given Binary Tree. 'lca' is lowest common ancestor of d1 and d2 Dist(d1, d2) is the distance between d1 and d2.
341 Views
