Data Structure
Data Structure Networking
Networking RDBMS
RDBMS Operating System
Operating System Java
Java MS Excel
MS Excel iOS
iOS HTML
HTML CSS
CSS Android
Android Python
Python C Programming
C Programming C++
C++ C#
C# MongoDB
MongoDB MySQL
MySQL Javascript
Javascript PHP
PHP
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
C++ Program to Check the Connectivity of Undirected Graph Using BFS
The Breadth-First Search (BFS) algorithm is a graph traversal algorithm that starts at the tree root and explores all nodes at the present depth before moving to the nodes at the next level. In this article, we will discuss how to check the connectivity of a graph using BFS traversal algorithm.
Understanding Connectivity of a Graph
A graph is said to be connected if there is a path between every pair of vertices. To check connectivity of a graph, we will try to traverse all nodes using any traversal algorithm. After completing the traversal, if there is any node, which is not visited, then the graph is not connected. To check this using BFS traversal,
- Start BFS traversal from any node (say node 0).
- Track visited vertices using a visited[] array.
- After BFS, if all vertices are visited, the graph is connected. And, if any vertex remains unvisited, the graph is disconnected.
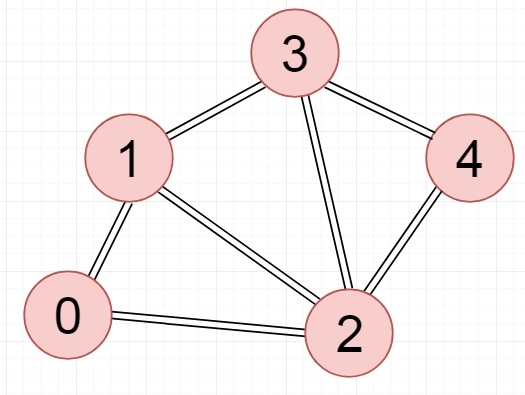
Connected Graph Example
The image below shows an example of a connected graph.
Algorithm: Checking Connectivity of a Graph
- Step 1: Start
- Step 2: Input number of vertices V and number of edges E
- Step 3: Create an adjacency list for the graph
- Step 4: For each edge, input the pair of vertices (u, v) and add them to each other's adjacency list
- Step 5: Initialize a visited array of size V with all values set to false
- Step 6: Initialize a queue for BFS traversal
- Step 7: Mark the starting node (vertex 0) as visited
- Step 8: Push the starting node into the queue
- Step 9: While the queue is not empty, repeat steps 10 to 12
- Step 10: Pop a vertex from the queue
- Step 11: For each adjacent vertex of the popped vertex, check if it is unvisited
- Step 12: If unvisited, mark it as visited and enqueue it
- Step 13: After BFS, check if all vertices are visited
- Step 14: If all are visited, the graph is connected; otherwise, it's disconnected
- Step 15: End
C++ Program: Checking Connectivity of a Graph
The following C++ program demonstrates how to check the connectivity of a graph using BFS. The program allows the user to input the number of vertices and edges, and then it displays whether the graph is connected or not.
#include <iostream>
#include <vector>
#include <queue>
using namespace std;
void addEdge(vector<int> adj[], int u, int v) {
adj[u].push_back(v);
adj[v].push_back(u); // Since the graph is undirected
}
bool isConnected(vector<int> adj[], int V) {
vector<bool> visited(V, false);
queue<int> q;
// Step 6: Start BFS from vertex 0
visited[0] = true;
q.push(0);
while (!q.empty()) {
int u = q.front();
q.pop();
for (int v : adj[u]) {
if (!visited[v]) {
visited[v] = true;
q.push(v);
}
}
}
// Step 7: Check if all vertices were visited
for (bool v : visited) {
if (!v) return false;
}
return true;
}
int main() {
int V, E;
cout << "Enter number of vertices: ";
cin >> V;
cout << "Enter number of edges: ";
cin >> E;
vector<int> adj[V];
cout << "Enter edges (u v):" << endl;
for (int i = 0; i < E; ++i) {
int u, v;
cin >> u >> v;
addEdge(adj, u, v);
}
if (isConnected(adj, V))
cout << "The graph is connected.\n";
else
cout << "The graph is not connected.\n";
return 0;
}
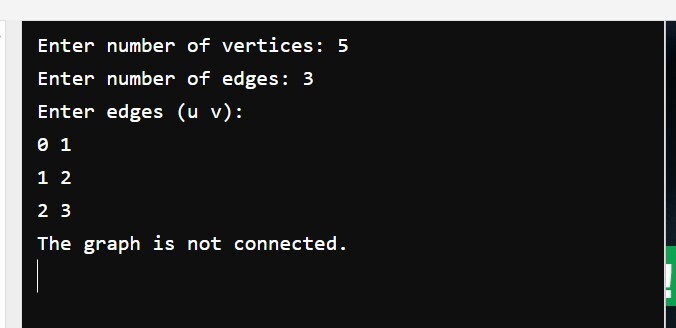
Sample Output
The output of the above program is as follows: