Centroid

Introduction

The centroid in mathematics designates the geometric centre of a planar surface with two dimensions. In this tutorial, we will learn about Centroid, and other centres of triangles and the relationship between them.

What is Centroid?

The centroid in mathematics designates the geometric centre of a planar surface with two dimensions. It is a point that is determined by taking the arithmetic mean of all the points on the plane surface as its location. The term "centroid" also refers to the centre of gravity.

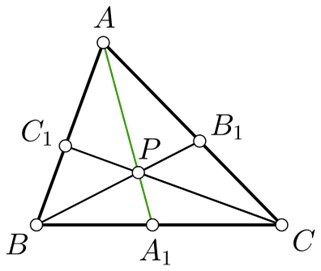
Locating centroid of triangle − The point where the triangle's three medians intersect is known as the centroid. A triangle's median is a line segment that connects a vertex to the middle of the side directly across from it.

For the triangle ABC, having AA₁,BB₁,& CC₁ as median, the centroid denoted by p looks like.

Other centres of the triangle

The triangle has three different types of centres other than centroid namely Orthocentre, Incentre and Circumcentre.

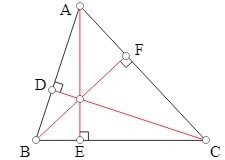
• Orthocentre − The intersection of altitudes traced perpendicularly from a triangle's vertices to its opposite sides is known as orthocentre.

  Orthocentre may lie inside or outside of the triangle depending on the type of triangle.

Here in the above figure, the intersection of all three altitudes is orthocentre.

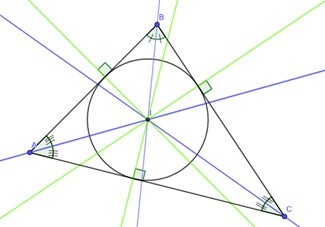
• Incentre − The intersection of the triangle's three interior angle bisectors forms the triangle's incentre.

  The centre of a triangle's incircle, which is inscribed in a triangle, is also referred to as the incentre of a triangle.

Here in the above figure, the intersection of all three interior angle bisectors is incentre, denoted by I.

• Circumcentre − The circumcentre of a triangle can be found out as the intersection of the perpendicular bisectors of all sides of the triangle.

  Each of the triangle's vertices is equidistant from the circumcentre.

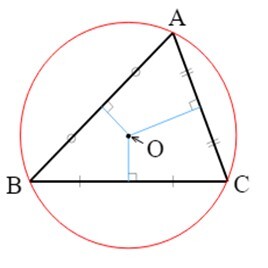
Here in the above figure, the intersection of all three perpendicular bisectors is circumcentre, denoted by O.

Properties of Centroid

• The geometric centre of the object is another name for the centroid.

• The arithmetic mean position of all the points in a flat figure is known as the centroid or geometric centre of the figure.

• A triangle's centroid is always contained within a triangle as the median lies inside of the triangle.

• By averaging the x and y coordinates of the triangle's three sides, the centroid can be determined.

• The most frequent point of concurrency inside a triangle is its centroid. Its significance in both mathematics and physics stems from the fact that it is the triangle's geometric centre.

• The centroid divides the medians into a 2:1 ratio.

  • With the longest segment closest to the vertex, the centroid divides each median into two segments with lengths that are 2:1.

• Centroid Theorem: The centroid of the triangle is at 2/3 of the distance from the vertex to the midpoint of the sides.

  • For the triangle ABC, having A¹,B¹,& C¹ as median, the centroid p

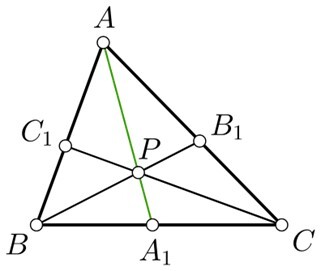
• Here using centroid theorem, $\mathrm{AP=\frac{2}{3} AA_1}$

• Similarly, $\mathrm{BP=\frac{2}{3} BB_1\:and\: CP=\frac{2}{3} CC_1}$

The Coordinate of the centroid of the triangle

The coordinate of the centroid can be calculated by taking the average values of the vertices of the triangle.

For the triangle ABC, having A¹,B¹,& C¹ as median and let the coordinate for A vertice be (x¹,y¹), for B vertice be (x²,y²), and for C vertice be (x³,y³) then

coordinate of the centroid is $C=(\frac{x_1+x_2+x_3}{3},\frac{y_1+y_2+y_3}{3}).$

Derivation of a coordinate of centroid

In the above triangle ABC and let the coordinate for A vertice be (x¹,y¹), for A vertice be (x²,y²), and for C vertice be (x³,y³)

Here the triangle have midpoints as A¹,B¹,& C¹ for the sides BC, AC and AB respectively, as we know that the median divides the side of the triangle into two equal parts.

Now by applying the midpoint formula for A¹, coordinates of A¹ will be, $\mathrm{(\frac{x_2+x_3}{2},\frac{y_2+y_3}{2})}$

Now by property of the centroid, as discussed above, the centroid divides the medians into a 2:1 ratio, so we can use the section formula.

Let P be the centroid of triangle ABC,

$$\mathrm{P=(\frac{\frac{2(x_2+x_3)}{2}+1(x_1)}{2+1},\frac{\frac{2(y_2+y_3)}{2}+1(y_3)}{2+1})}$$

on simplifying,

$$\mathrm{P=(\frac{x_1+x_2+x_3}{3},\frac{y_1+y_2+y_3}{3})}$$

Equilateral triangle

Equilateral triangles are those with equal lengths on all three sides. The centre of the triangle is where the centroid of the equilateral triangle is located.

Draw perpendicular lines from each triangle vertex to the opposing sides in order to get the centroid. The centroid is the place where all of these perpendiculars, which are all equal in length, intersect.

The median, angle bisector, and altitude of an equilateral triangle are all the same. Thus, all the centres are the same in an equilateral triangle.

The distance between the centroid to any vertex of the equilateral triangle can be calculated as −

Let a be the length of any side in an equilateral triangle, and by properties of the equilateral triangle, we know that the height of an equilateral triangle is,

$$\mathrm{h=\frac{√3}{2} a}$$

and by properties of the centroid, we know that the centroid divides the medians into a 2:1 ratio.

Consequently, the equilateral triangle's centroid's distance from any of its vertices

=2/3 of the equilateral triangle's height =$\mathrm{\frac{2}{3}×\frac{√3}{2} a}$

$$\mathrm{=\frac{a}{√3}.}$$

Solved examples

1)Find the centroid for a triangle having coordinates as P(15,4),Q(4,-6),R(5,12)

The formula to find the coordinate of the centroid is, $\mathrm{C=(\frac{x_1+x_2+x_3}{3},\frac{y_1+y_2+y_3}{3})}$

Therefore, here we have x_1=15, x_2=4,x_3=5 and y_1=4,y_2=-6,y_3=12

Substituting these values in above formula for C, we have

$$\mathrm{C=(\frac{15+4+5}{3},\frac{4-6+12}{3})=(\frac{24}{3},\frac{10}{3})}$$

Therefore, the coordinates of centroid are, $\mathrm{(8,\frac{10}{3})}$.

2)Find the centroid for a triangle having coordinates as A(-3,3),B(3,1),C(-1,-1)

The formula to find coordinate of centroid is, $\mathrm{C=(\frac{x_1+x_2+x_3}{3},\frac{y_1+y_2+y_3}{3})}$

Therefore, here we have x₁=-3, x₂=3,x₃=-1 and y₁=3,y₂=1,y₃=-1

Substituting these values in above formula for C, we have

$$\mathrm{C=(\frac{-3+3-1}{3},\frac{3+1-1}{3})=(\frac{-1}{3},\frac{3}{3})}$$

Therefore, the coordinates of the centroid are, $\mathrm{(\frac{-1}{3},1).}$

Conclusion

The centroid in mathematics designates the geometric centre of a planar surface with two dimensions. Three medians of a triangle intersect to produce the centroid of the triangle. It is one of a triangle's four points of concurrency. The angle bisectors' intersection is at the incentre. While the medians' intersection is known as the centroid. Although the centroid divides its median into a ratio of 2:1, incentre does not specifically divide the angle bisectors. Both the incentre and centroid lie inside the triangle.

FAQs

1. What is the centroid of a triangle?

Three medians of a triangle intersect to produce the centroid of the triangle. It is one of a triangle's four points of concurrency. Centroid is in fact the geometric centre of a triangle.

2. What is the centroid Theorem?

The centroid theorem states that the centroid of the triangle is at 2/3 of the distance from the vertex to the midpoint of the sides.

3. What is the difference between centroid and incentre?

The angle bisectors' intersection is at the incentre. While the medians' intersection is known as the centroid. Although the centroid divides its median into a ratio of 2:1, incentre does not specifically divide the angle bisectors. Both the incentre and centroid lie inside the triangle.

4. What is the difference between centroid and orthocentre?

The altitudes' intersection is at the orthocentre. While the medians' intersection is known as the centroid, although the centroid divides its median into a ratio of 2:1, the orthocentre does not specifically divide the angle bisectors. The orthocentre lies outside, and the centroid lies inside the triangle.

5. What is the formula for calculating centroid?

The coordinate of the centroid can be calculated by taking the average values of the vertices of the triangle. For the triangle ABC, let the coordinate for A vertice be (x₁,y₁)for B vertice be (x₂,y₂), and for C vertice be (x₃,y₃) then coordinate of the centroid are

$$\mathrm{C=(\frac{x_1+x_2+x_3}{3},\frac{y_1+y_2+y_3}{3}).}$$