Centered Triangular Number

What do you understand by the term centered triangular number? Let’s decode in this article.

First, what is a triangular number?

A triangular arrangement of objects or dots can be used to represent a particular kind of figurate number known as a triangular number. The sum of the first n natural numbers is the nth triangular number.

The first few triangular numbers, for instance, are:

1, 3, 6, 10, 15, 21

You can view these figures as triangular clusters of dots to demonstrate how they were calculated, as seen below:

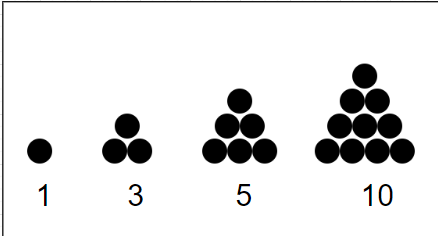
If you take a closer look you will see:

1 = 1

3 = 1 + 2

6 = 1 + 2 + 3

10 = 1+ ….+4

15= 1+ ……+5

21= 1+2+3+4+5+6

Hence we can conclude that, The formula for finding the nth triangular number is n(n+1)/2.

Now, what is a centered triangular number?

A centered triangular number is a type of triangular number that is formed by placing a single dot in the center of a regular triangle of dots. The first few centered triangular numbers are:

1, 4, 10, 19, 31, 46, 64, 85, 109, 136, 166,...

Now, look at the diagram below.

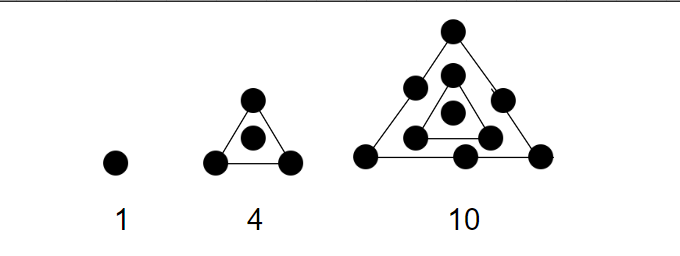
The formula to calculate nth centered triangle is C_n= 1 + 3(n(n+1)/2) = (3n^2+ 3n+2)/2

Approach

Now, you know what is centered triangular number. Let’s discuss the approach to write c++ code for the same.

• Specify the value of n, or take it as user input.

• Use the formula (3n^2+ 3n+2)/2 to calculate the nth centered triangular number.

• Print the value to the console.

C++ Code Implementation

Too much theory? Let’s get into the code mode. Here is the c++ code implementation of the above approach to calculate the nth centered triangular number.

Example

#include <iostream>
using namespace std;

int main() {
    int n= 10;

    int centered_triangular = (3*n*n + 3*n + 2)/2;
    cout << "The " << n << "th centered triangular number is: " << centered_triangular << endl;

    return 0;
}

Output

The 10th centered triangular number is: 166

Time Complexity: O(1)

Space Complexity: O(1)

Conclusion

In this article we covered what is triangular number and what is centered triangular number. We also explored the logic behind calculating the nth centered triangular number and to convert it into c++ code. Hope you have a clear idea of the concept now and you found the article helpful.