
- DSA - Home
- DSA - Overview
- DSA - Environment Setup
- DSA - Algorithms Basics
- DSA - Asymptotic Analysis
- Data Structures
- DSA - Data Structure Basics
- DSA - Data Structures and Types
- DSA - Array Data Structure
- DSA - Skip List Data Structure
- Linked Lists
- DSA - Linked List Data Structure
- DSA - Doubly Linked List Data Structure
- DSA - Circular Linked List Data Structure
- Stack & Queue
- DSA - Stack Data Structure
- DSA - Expression Parsing
- DSA - Queue Data Structure
- DSA - Circular Queue Data Structure
- DSA - Priority Queue Data Structure
- DSA - Deque Data Structure
- Searching Algorithms
- DSA - Searching Algorithms
- DSA - Linear Search Algorithm
- DSA - Binary Search Algorithm
- DSA - Interpolation Search
- DSA - Jump Search Algorithm
- DSA - Exponential Search
- DSA - Fibonacci Search
- DSA - Sublist Search
- DSA - Hash Table
- Sorting Algorithms
- DSA - Sorting Algorithms
- DSA - Bubble Sort Algorithm
- DSA - Insertion Sort Algorithm
- DSA - Selection Sort Algorithm
- DSA - Merge Sort Algorithm
- DSA - Shell Sort Algorithm
- DSA - Heap Sort Algorithm
- DSA - Bucket Sort Algorithm
- DSA - Counting Sort Algorithm
- DSA - Radix Sort Algorithm
- DSA - Quick Sort Algorithm
- Matrices Data Structure
- DSA - Matrices Data Structure
- DSA - Lup Decomposition In Matrices
- DSA - Lu Decomposition In Matrices
- Graph Data Structure
- DSA - Graph Data Structure
- DSA - Depth First Traversal
- DSA - Breadth First Traversal
- DSA - Spanning Tree
- DSA - Topological Sorting
- DSA - Strongly Connected Components
- DSA - Biconnected Components
- DSA - Augmenting Path
- DSA - Network Flow Problems
- DSA - Flow Networks In Data Structures
- DSA - Edmonds Blossom Algorithm
- DSA - Maxflow Mincut Theorem
- Tree Data Structure
- DSA - Tree Data Structure
- DSA - Tree Traversal
- DSA - Binary Search Tree
- DSA - AVL Tree
- DSA - Red Black Trees
- DSA - B Trees
- DSA - B+ Trees
- DSA - Splay Trees
- DSA - Range Queries
- DSA - Segment Trees
- DSA - Fenwick Tree
- DSA - Fusion Tree
- DSA - Hashed Array Tree
- DSA - K-Ary Tree
- DSA - Kd Trees
- DSA - Priority Search Tree Data Structure
- Recursion
- DSA - Recursion Algorithms
- DSA - Tower of Hanoi Using Recursion
- DSA - Fibonacci Series Using Recursion
- Divide and Conquer
- DSA - Divide and Conquer
- DSA - Max-Min Problem
- DSA - Strassen's Matrix Multiplication
- DSA - Karatsuba Algorithm
- Greedy Algorithms
- DSA - Greedy Algorithms
- DSA - Travelling Salesman Problem (Greedy Approach)
- DSA - Prim's Minimal Spanning Tree
- DSA - Kruskal's Minimal Spanning Tree
- DSA - Dijkstra's Shortest Path Algorithm
- DSA - Map Colouring Algorithm
- DSA - Fractional Knapsack Problem
- DSA - Job Sequencing with Deadline
- DSA - Optimal Merge Pattern Algorithm
- Dynamic Programming
- DSA - Dynamic Programming
- DSA - Matrix Chain Multiplication
- DSA - Floyd Warshall Algorithm
- DSA - 0-1 Knapsack Problem
- DSA - Longest Common Sub-sequence Algorithm
- DSA - Travelling Salesman Problem (Dynamic Approach)
- Hashing
- DSA - Hashing Data Structure
- DSA - Collision In Hashing
- Disjoint Set
- DSA - Disjoint Set
- DSA - Path Compression And Union By Rank
- Heap
- DSA - Heap Data Structure
- DSA - Binary Heap
- DSA - Binomial Heap
- DSA - Fibonacci Heap
- Tries Data Structure
- DSA - Tries
- DSA - Standard Tries
- DSA - Compressed Tries
- DSA - Suffix Tries
- Treaps
- DSA - Treaps Data Structure
- Bit Mask
- DSA - Bit Mask In Data Structures
- Bloom Filter
- DSA - Bloom Filter Data Structure
- Approximation Algorithms
- DSA - Approximation Algorithms
- DSA - Vertex Cover Algorithm
- DSA - Set Cover Problem
- DSA - Travelling Salesman Problem (Approximation Approach)
- Randomized Algorithms
- DSA - Randomized Algorithms
- DSA - Randomized Quick Sort Algorithm
- DSA - Karger’s Minimum Cut Algorithm
- DSA - Fisher-Yates Shuffle Algorithm
- Miscellaneous
- DSA - Infix to Postfix
- DSA - Bellmon Ford Shortest Path
- DSA - Maximum Bipartite Matching
- DSA Useful Resources
- DSA - Questions and Answers
- DSA - Selection Sort Interview Questions
- DSA - Merge Sort Interview Questions
- DSA - Insertion Sort Interview Questions
- DSA - Heap Sort Interview Questions
- DSA - Bubble Sort Interview Questions
- DSA - Bucket Sort Interview Questions
- DSA - Radix Sort Interview Questions
- DSA - Cycle Sort Interview Questions
- DSA - Quick Guide
- DSA - Useful Resources
- DSA - Discussion
B+ Trees
The B+ trees are extensions of B trees designed to make the insertion, deletion and searching operations more efficient.
The properties of B+ trees are similar to the properties of B trees, except that the B trees can store keys and records in all internal nodes and leaf nodes while B+ trees store records in leaf nodes and keys in internal nodes. One profound property of the B+ tree is that all the leaf nodes are connected to each other in a single linked list format and a data pointer is available to point to the data present in disk file. This helps fetch the records in equal numbers of disk access.
Since the size of main memory is limited, B+ trees act as the data storage for the records that couldnt be stored in the main memory. For this, the internal nodes are stored in the main memory and the leaf nodes are stored in the secondary memory storage.
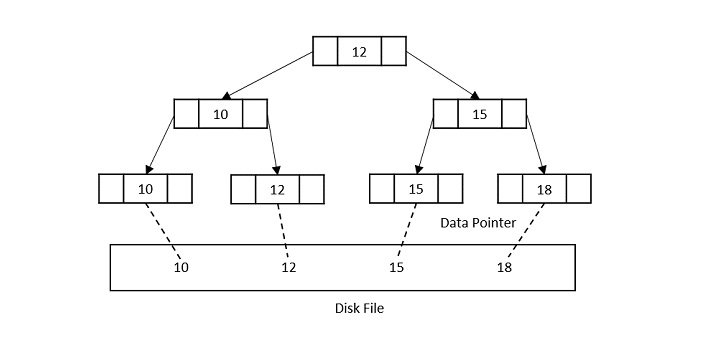
Properties of B+ trees
Every node in a B+ Tree, except root, will hold a maximum of m children and (m-1) keys, and a minimum of $\mathrm{\left \lceil \frac{m}{2}\right \rceil}$ children and $\mathrm{\left \lceil \frac{m-1}{2}\right \rceil}$ keys, since the order of the tree is m.
The root node must have no less than two children and at least one search key.
All the paths in a B tree must end at the same level, i.e. the leaf nodes must be at the same level.
A B+ tree always maintains sorted data.
Basic Operations of B+ Trees
The operations supported in B+ trees are Insertion, deletion and searching with the time complexity of O(log n) for every operation.
They are almost similar to the B tree operations as the base idea to store data in both data structures is same. However, the difference occurs as the data is stored only in the leaf nodes of a B+ trees, unlike B trees.
Insertion operation
The insertion to a B+ tree starts at a leaf node.
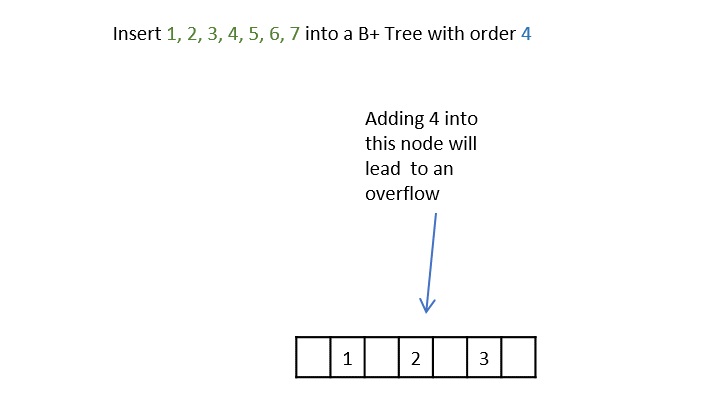
Step 1 − Calculate the maximum and minimum number of keys to be added onto the B+ tree node.

Step 2 − Insert the elements one by one accordingly into a leaf node until it exceeds the maximum key number.
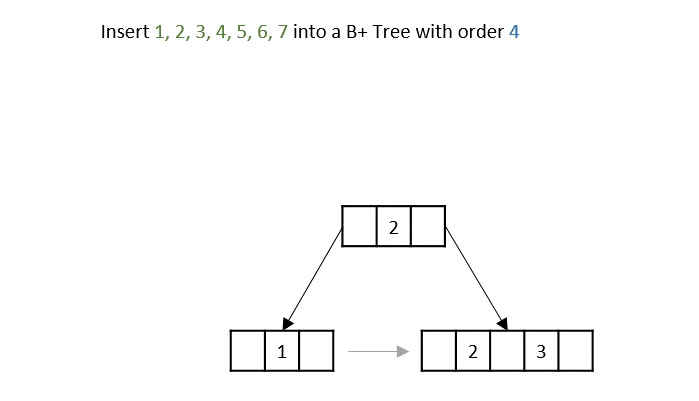
Step 3 − The node is split into half where the left child consists of minimum number of keys and the remaining keys are stored in the right child.
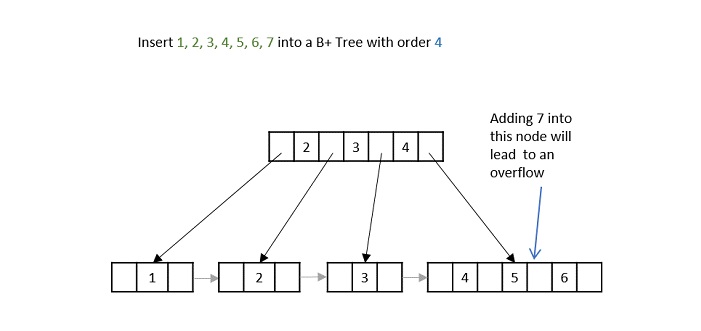
Step 4 − But if the internal node also exceeds the maximum key property, the node is split in half where the left child consists of the minimum keys and remaining keys are stored in the right child. However, the smallest number in the right child is made the parent.
Step 5 − If both the leaf node and internal node have the maximum keys, both of them are split in the similar manner and the smallest key in the right child is added to the parent node.
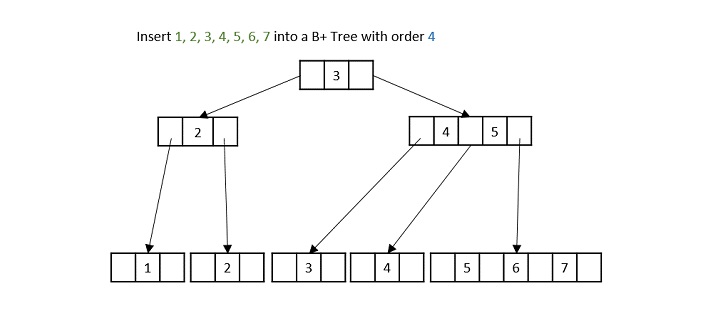
Example
Following are the implementations of this operation in various programming languages −
// C program for Bplus tree
#include <stdio.h>
#include <stdlib.h>
struct BplusTree {
int *d;
struct BplusTree **child_ptr;
int l;
int n;
};
struct BplusTree *r = NULL, *np = NULL, *x = NULL;
struct BplusTree* init() {
//to create nodes
int i;
np = (struct BplusTree*)malloc(sizeof(struct BplusTree));
np->d = (int*)malloc(6 * sizeof(int)); // order 6
np->child_ptr = (struct BplusTree**)malloc(7 * sizeof(struct BplusTree*));
np->l = 1;
np->n = 0;
for (i = 0; i < 7; i++) {
np->child_ptr[i] = NULL;
}
return np;
}
void traverse(struct BplusTree *p) {
//traverse tree
printf("\n");
int i;
for (i = 0; i < p->n; i++) {
if (p->l == 0) {
traverse(p->child_ptr[i]);
}
printf(" %d", p->d[i]);
}
if (p->l == 0) {
traverse(p->child_ptr[i]);
}
printf("\n");
}
void sort(int *p, int n) {
int i, j, t;
for (i = 0; i < n; i++) {
for (j = i; j <= n; j++) {
if (p[i] > p[j]) {
t = p[i];
p[i] = p[j];
p[j] = t;
}
}
}
}
int split_child(struct BplusTree *x, int i) {
int j, mid;
struct BplusTree *np1, *np3, *y;
np3 = init();
np3->l = 1;
if (i == -1) {
mid = x->d[2];
x->d[2] = 0;
x->n--;
np1 = init();
np1->l = 0;
x->l = 1;
for (j = 3; j < 6; j++) {
np3->d[j - 3] = x->d[j];
np3->child_ptr[j - 3] = x->child_ptr[j];
np3->n++;
x->d[j] = 0;
x->n--;
}
for (j = 0; j < 6; j++) {
x->child_ptr[j] = NULL;
}
np1->d[0] = mid;
np1->child_ptr[np1->n] = x;
np1->child_ptr[np1->n + 1] = np3;
np1->n++;
r = np1;
} else {
y = x->child_ptr[i];
mid = y->d[2];
y->d[2] = 0;
y->n--;
for (j = 3; j < 6; j++) {
np3->d[j - 3] = y->d[j];
np3->n++;
y->d[j] = 0;
y->n--;
}
x->child_ptr[i + 1] = y;
x->child_ptr[i + 1] = np3;
}
return mid;
}
void insert(int a) {
int i, t;
x = r;
if (x == NULL) {
r = init();
x = r;
} else {
if (x->l == 1 && x->n == 6) {
t = split_child(x, -1);
x = r;
for (i = 0; i < x->n; i++) {
if (a > x->d[i] && a < x->d[i + 1]) {
i++;
break;
} else if (a < x->d[0]) {
break;
} else {
continue;
}
}
x = x->child_ptr[i];
} else {
while (x->l == 0) {
for (i = 0; i < x->n; i++) {
if (a > x->d[i] && a < x->d[i + 1]) {
i++;
break;
} else if (a < x->d[0]) {
break;
} else {
continue;
}
}
if (x->child_ptr[i]->n == 6) {
t = split_child(x, i);
x->d[x->n] = t;
x->n++;
continue;
} else {
x = x->child_ptr[i];
}
}
}
}
x->d[x->n] = a;
sort(x->d, x->n);
x->n++;
}
int main() {
int i, n, t;
insert(10);
insert(20);
insert(30);
insert(40);
insert(50);
printf("Insertion Done");
printf("\nB+ tree:");
traverse(r);
return 0;
}
Output
Insertion Done B+ tree: 10 20 30 40 50
#include<iostream>
using namespace std;
struct BplusTree {
int *d;
BplusTree **child_ptr;
bool l;
int n;
}
*r = NULL, *np = NULL, *x = NULL;
BplusTree* init() { //to create nodes
int i;
np = new BplusTree;
np->d = new int[6];//order 6
np->child_ptr = new BplusTree *[7];
np->l = true;
np->n = 0;
for (i = 0; i < 7; i++) {
np->child_ptr[i] = NULL;
}
return np;
}
void traverse(BplusTree *p) { //traverse tree
cout<<endl;
int i;
for (i = 0; i < p->n; i++) {
if (p->l == false) {
traverse(p->child_ptr[i]);
}
cout << " " << p->d[i];
}
if (p->l == false) {
traverse(p->child_ptr[i]);
}
cout<<endl;
}
void sort(int *p, int n) { //sort the tree
int i, j, t;
for (i = 0; i < n; i++) {
for (j = i; j <= n; j++) {
if (p[i] >p[j]) {
t = p[i];
p[i] = p[j];
p[j] = t;
}
}
}
}
int split_child(BplusTree *x, int i) {
int j, mid;
BplusTree *np1, *np3, *y;
np3 = init();
np3->l = true;
if (i == -1) {
mid = x->d[2];
x->d[2] = 0;
x->n--;
np1 = init();
np1->l = false;
x->l = true;
for (j = 3; j < 6; j++) {
np3->d[j - 3] = x->d[j];
np3->child_ptr[j - 3] = x->child_ptr[j];
np3->n++;
x->d[j] = 0;
x->n--;
}
for (j = 0; j < 6; j++) {
x->child_ptr[j] = NULL;
}
np1->d[0] = mid;
np1->child_ptr[np1->n] = x;
np1->child_ptr[np1->n + 1] = np3;
np1->n++;
r = np1;
} else {
y = x->child_ptr[i];
mid = y->d[2];
y->d[2] = 0;
y->n--;
for (j = 3; j <6 ; j++) {
np3->d[j - 3] = y->d[j];
np3->n++;
y->d[j] = 0;
y->n--;
}
x->child_ptr[i + 1] = y;
x->child_ptr[i + 1] = np3;
}
return mid;
}
void insert(int a) {
int i, t;
x = r;
if (x == NULL) {
r = init();
x = r;
} else {
if (x->l== true && x->n == 6) {
t = split_child(x, -1);
x = r;
for (i = 0; i < (x->n); i++) {
if ((a >x->d[i]) && (a < x->d[i + 1])) {
i++;
break;
} else if (a < x->d[0]) {
break;
} else {
continue;
}
}
x = x->child_ptr[i];
} else {
while (x->l == false) {
for (i = 0; i < (x->n); i++) {
if ((a >x->d[i]) && (a < x->d[i + 1])) {
i++;
break;
} else if (a < x->d[0]) {
break;
} else {
continue;
}
}
if ((x->child_ptr[i])->n == 6) {
t = split_child(x, i);
x->d[x->n] = t;
x->n++;
continue;
} else {
x = x->child_ptr[i];
}
}
}
}
x->d[x->n] = a;
sort(x->d, x->n);
x->n++;
}
int main() {
int i, n, t;
insert(10);
insert(20);
insert(30);
insert(40);
insert(50);
cout<<"Insertion Done";
cout<<"\nB+ tree:";
traverse(r);
}
Output
Insertion Done B+ tree: 10 20 30 40 50
//Java program for Bplus code
import java.util.*;
class BplusTree {
int[] d;
BplusTree[] child_ptr;
boolean l;
int n;
}
public class Main {
static BplusTree r = null, np = null, x = null;
static BplusTree init() { // to create nodes
int i;
np = new BplusTree();
np.d = new int[6]; // order 6
np.child_ptr = new BplusTree[7];
np.l = true;
np.n = 0;
for (i = 0; i < 7; i++) {
np.child_ptr[i] = null;
}
return np;
}
static void traverse(BplusTree p) { // traverse tree
int i;
for (i = 0; i < p.n; i++) {
if (p.l == false) {
traverse(p.child_ptr[i]);
}
System.out.print(" " + p.d[i]);
}
if (p.l == false) {
traverse(p.child_ptr[i]);
}
System.out.println();
}
static void sort(int[] p, int n) { // sort the tree
int i, j, t;
for (i = 0; i < n; i++) {
for (j = i; j <= n; j++) {
if (p[i] > p[j]) {
t = p[i];
p[i] = p[j];
p[j] = t;
}
}
}
}
static int split_child(BplusTree x, int i) {
int j, mid;
BplusTree np1, np3, y;
np3 = init();
np3.l = true;
if (i == -1) {
mid = x.d[2];
x.d[2] = 0;
x.n--;
np1 = init();
np1.l = false;
x.l = true;
for (j = 3; j < 6; j++) {
np3.d[j - 3] = x.d[j];
np3.child_ptr[j - 3] = x.child_ptr[j];
np3.n++;
x.d[j] = 0;
x.n--;
}
for (j = 0; j < 6; j++) {
x.child_ptr[j] = null;
}
np1.d[0] = mid;
np1.child_ptr[np1.n] = x;
np1.child_ptr[np1.n + 1] = np3;
np1.n++;
r = np1;
} else {
y = x.child_ptr[i];
mid = y.d[2];
y.d[2] = 0;
y.n--;
for (j = 3; j < 6; j++) {
np3.d[j - 3] = y.d[j];
np3.n++;
y.d[j] = 0;
y.n--;
}
x.child_ptr[i + 1] = y;
x.child_ptr[i + 1] = np3;
}
return mid;
}
static void insert(int a) {
int i, t;
x = r;
if (x == null) {
r = init();
x = r;
} else {
if (x.l == true && x.n == 6) {
t = split_child(x, -1);
x = r;
for (i = 0; i < x.n; i++) {
if (a > x.d[i] && a < x.d[i + 1]) {
i++;
break;
} else if (a < x.d[0]) {
break;
} else {
continue;
}
}
x = x.child_ptr[i];
} else {
while (x.l == false) {
for (i = 0; i < x.n; i++) {
if (a > x.d[i] && a < x.d[i + 1]) {
i++;
break;
} else if (a < x.d[0]) {
break;
} else {
continue;
}
}
if (x.child_ptr[i].n == 6) {
t = split_child(x, i);
x.d[x.n] = t;
x.n++;
continue;
} else {
x = x.child_ptr[i];
}
}
}
}
x.d[x.n] = a;
sort(x.d, x.n);
x.n++;
}
public static void main(String[] args) {
int i, n, t;
insert(10);
insert(20);
insert(30);
insert(40);
insert(50);
System.out.print("Insertion Done");
System.out.println("\nB+ tree:");
traverse(r);
}
}
Output
Insertion Done B+ tree: 10 20 30 40 50
#Python Program for Bplus tree
#to create nodes
class BplusTree:
def __init__(self):
self.d = [0] * 6 # order 6
self.child_ptr = [None] * 7
self.l = True
self.n = 0
def init():
np = BplusTree()
np.l = True
np.n = 0
return np
#traverse tree
def traverse(p):
for i in range(p.n):
if not p.l:
traverse(p.child_ptr[i])
print(" ", p.d[i], end="")
if not p.l:
traverse(p.child_ptr[p.n])
print()
#sort the tree
def sort(p, n):
for i in range(n):
for j in range(i, n + 1):
if p[i] > p[j]:
p[i], p[j] = p[j], p[i]
def split_child(x, i):
np3 = init()
np3.l = True
if i == -1:
mid = x.d[2]
x.d[2] = 0
x.n -= 1
np1 = init()
np1.l = False
x.l = True
for j in range(3, 6):
np3.d[j - 3] = x.d[j]
np3.child_ptr[j - 3] = x.child_ptr[j]
np3.n += 1
x.d[j] = 0
x.n -= 1
for j in range(6):
x.child_ptr[j] = None
np1.d[0] = mid
np1.child_ptr[np1.n] = x
np1.child_ptr[np1.n + 1] = np3
np1.n += 1
r = np1
else:
y = x.child_ptr[i]
mid = y.d[2]
y.d[2] = 0
y.n -= 1
for j in range(3, 6):
np3.d[j - 3] = y.d[j]
np3.n += 1
y.d[j] = 0
y.n -= 1
x.child_ptr[i + 1] = y
x.child_ptr[i + 1] = np3
return mid
def insert(a):
global r, x
x = r
if x is None:
r = init()
x = r
else:
if x.l and x.n == 6:
t = split_child(x, -1)
x = r
for i in range(x.n):
if a > x.d[i] and a < x.d[i + 1]:
i += 1
break
elif a < x.d[0]:
break
else:
continue
x = x.child_ptr[i]
else:
while not x.l:
for i in range(x.n):
if a > x.d[i] and a < x.d[i + 1]:
i += 1
break
elif a < x.d[0]:
break
else:
continue
if x.child_ptr[i].n == 6:
t = split_child(x, i)
x.d[x.n] = t
x.n += 1
continue
else:
x = x.child_ptr[i]
x.d[x.n] = a
sort(x.d, x.n)
x.n += 1
r = None
x = None
insert(10)
insert(20)
insert(30)
insert(40)
insert(50)
print("Insertion Done")
print("B+ tree:")
traverse(r)
Output
Insertion Done B+ tree: 10 20 30 40 50
