Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
B-tree Deletion in Data Structure
Here we will see, how to perform the deletion of a node from B-Tree. Suppose we have a BTree like below −
Example of B-Tree −
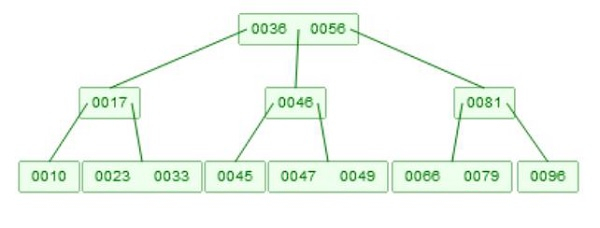
Deletion has two parts. At first we have to find the element. That strategy is like the querying. Now for deletion, we have to care about some rules. One node must have at-least m/2 elements. So if we delete, one element, and it has less than m-1 elements remaining, then it will adjust itself. If the entire node is deleted, then its children will be merged, and if their size issame as m, then split them into two parts, and again the median value will go up.
Suppose we want to delete 46. Now there are two children. [45], and [47, 49], then they will be merged, it will be [45, 47, 49], now 47 will go up.
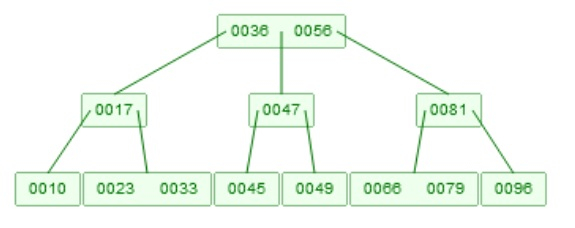
Algorithm
BTreeDelete(x, key) −
Input − The root of the tree, and key to delete
We will assume, that the key is present into the list
if x is leaf, then delete object with key ‘key’ from x else if x does not contain the object with key ‘key’, then locate the child x->child[i] whose key range is holding ‘key’ y := x->child[i] if y has m/2 elements, then If the sibling node z immediate to the left or right of y, has at least one more object than m/2, add one more object by moving x->key[i] from x to y, and move that last or first object from z to x. If y is non-leaf node, then last or first child pointer in z is also moved to y else any immediate sibling of y has m/2 elements, merge y with immediate sibling end if BTreeDelete(y, key) else if y that precedes ‘key’ in x, has at-least m/2 + 1 objects, then find predecessor k of ‘key’, in the sub-tree rooted by y. then recursively delete k from the sub-tree and replace key with k in x else if ys has m/2 elements, then check the child z, which is immediately follows ‘key’ in x if z has at least m/2+1 elements, then find successor k of ‘key’, in the sub-tree rooted by z. recursively delete k from sub-tree, and replace key with k in x else both y and z has m/2 elements, then merge then into one node, and push ‘key’ down to the new node as well. Recursively delete ‘key’ from this new node end if end if
871 Views
