B-tree Insertion in Data Structure

Here we will see, how to perform the insertion into a B-Tree. Suppose we have a B-Tree like below −

Example of B-Tree −

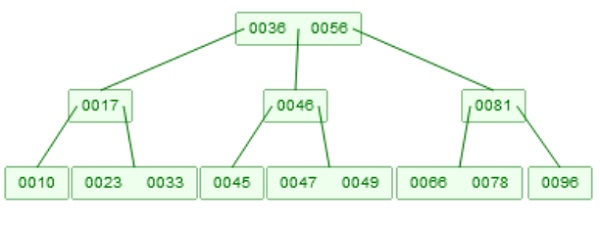
To insert an element, the idea is very similar to the BST, but we have to follow some rules. Each node has m children, and m-1 elements. If we insert an element into one node, there are two situations. If the node has elements less than m-1, then the new element will be inserted directly into the node. If it has m-1 elements, then by taking all elements, and the element which will be inserted, then take the median of them, and the median value is send to the root of that node by performing the same criteria, then create two separate lists from left half and right half of the node

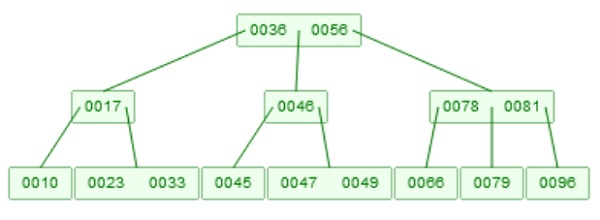
Suppose we want to insert 79 into the tree. At first it will be checked with root, this is greater than 56. Then it will come to the right most sub-tree. Now it is less than 81, so move to the left sub-tree. After that it will be inserted into the root. Now there are three elements [66, 78, 79]. The median value is 78, so 78 will go up, and the root node becomes [79, 81], and the elements of the node will be split into two nodes. One will hold 66, and another will hold 79.

B-Tree after inserting 79.

Algorithm

BTreeInsert(root, key)− 

Input − The root of the tree, and key to insert We will assume, that the key is not present into the list

x := Read root
if x is full, then
   y := new node
   z := new node
   Locate the middle object oi, stored in x, move the objects to the left of oi in to node y
   Move the object to the right of oi into node z.
   If x is an index node, then move the child pointers accordingly
   x->child[1] := address of y
   x->child[2] := address of z
end if