Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
The B-tree in Data Structure
Here we will see what are the B-Trees. The B-Trees are specialized m-way search tree. This can be widely used for disc access. A B-tree of order m, can have maximum m-1 keys and m children. This can store large number of elements in a single node. So the height is relatively small. This is one great advantage of B-Trees.
B-Tree has all of the properties of one m-way tree. It has some other properties.
Every node in B-Tree will hold maximum m children
Every node except root and leaves, can hold at least m/2 children
The root nodes must have at least two children.
All leaf nodes must have at same level
Example of B-Tree
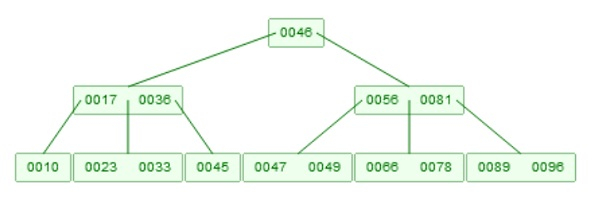
This supports basic operations like searching, insertion, deletion. In each node, the item will be sorted. The element at position i has child before and after it. So children sored before will hold smaller values, and children present at right will hold bigger values.
3K+ Views
