Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Insertion in the Red Black Tree in Data Structure
Red Black Tree is a Self-Balanced Binary Search Tree in which each node of the tree is colored with either Red or Black. There are three types of operations we can perform on a Red Black Tree – Searching, Insertion and Deletion.
Let us suppose we have to insert an element in the following Red Black Tree.
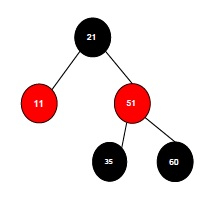
To insert an element in a red-black tree the idea is very simple − we perform insertion just like we insert in a regular binary tree. We start off from the root node by checking the color of the node and insert it into a particular position. However, In a red-black tree there should be some additional procedure to insert an element in it.
However, we should know that a red-black tree is balanced when it follows the conditions −
Every Root Node must be Black.
Every node is either Red or Black.
If a node is red, then its children must be black.
The path from the root till the end must contain an equal number of black nodes.
If we want to insert a new node in a red-black tree, then we can do it by looking at the insertion steps.
Steps to Insert an Element in a Red Black Tree −
Check whether the tree is empty or not. If the tree is empty, then insert a new node and color it as Black. (Because Root Node must be always Black in color)’
Otherwise if the Tree is not empty then insert the new node as a leaf node to the end and color it as Red.
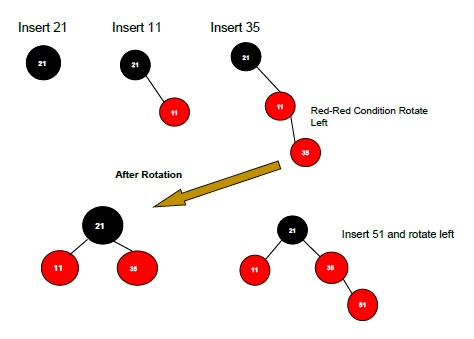
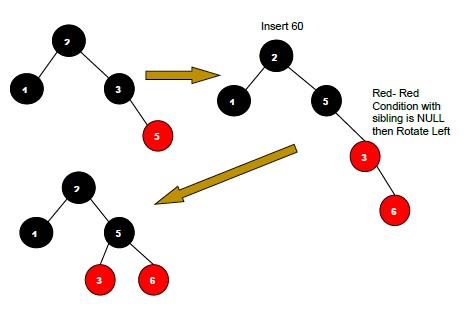
If the parent of the new node is Red and its neighbouring(parent’s) node is also Red then Flip the color of the both neighbour and Parent and Grandparents (If it is not Root Node Otherwise Flip the color of the Parent and neighbour only) i.e., Black.
If the parent of the new node is Red and its neighbouring(parent’s) node is empty or NULL, then Rotate (either Left-Left or Left-Right rotation) the new node and parent.
There are two types of rotation that would apply- Left Left Rotation and Left Right Rotation. The Rotation would apply in some conditions only. The conditions are −
If the parent of the new node is Red and the neighbouring node is empty or NULL, then rotate left or right rotation.
In Left-Left Rotation flip the color of the parent and grandparent. Make the parent as Grandparent and grandparent as child.
Algorithm
RBTreeInsertion(root,key)
//The color of the inserted new node is Red color[key] <- Red while(key≠root and color (p[key]=Red)) do if p[key]= left(p[p[key]]) Then y←right[p[p[key]] // If the parent of the new node is Red(if there is Grandparent instead root Node) Flip the color. if color[y]← Red then color(p[key])← Black color(p[p[key]])← Red key← p[p[key]] else if key← right[p[key]] then key← p[key] //When parent of new node has the red color and its sibling is NULL LeftRotate(root,key) color(p[key]) ← Black color(p[p[key]]) ← Red RotateRight(root,p[p[key]]) else exchange then left and right elements to make it balance. color(root)← Black
7K+ Views
