Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
B+ tree Deletion in Data Structure
Here we will see, how to perform the deletion of a node from B+ Tree. Suppose we have a B+ Tree like below 7minus;
Example of B+ Tree −
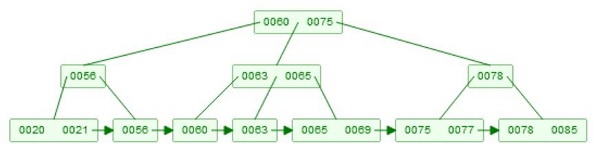
Deletion has two parts. At first we have to find the element. That strategy is like the querying. Now for deletion, we have to care about some rules. One node must have at-least m/2 elements. So if we delete, one element, and it has less than m-1 elements remaining, then it will adjust itself. If the entire node is deleted, then its children will be merged, and if their size is same as m, then split them into two parts, and again the median value will go up.
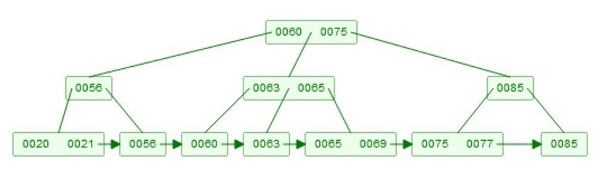
Suppose we want to delete 78. Now there are two children. [75, 77], and [78, 85], then It will delete 78 from the leaf node first, after that take 85, and make a copy of key 85, and make it as root of the subtree.
Algorithm
BPlusTreeDelete(x, key) −
Input − The root of the tree, and key to delete
We will assume, that the key is present into the list Start from root node, perform exact match for key as ‘key’ till a leaf node. Let the search path be x1, x2, … , xh. The x1 is first node so root, then xh is leaf node. Each node xi is parent of xi+1 delete the object where key is ‘key’ from xh. if h = 1, then return, as there is only one node which is root. i := h while xi underflows, do if immediate sibling node s of xi, has at least m/2 + 1 elements, then redistribute entries evenly between s and xi. corresponding to redistribution, a key k in the parent node xi-1, will be changed. if xi is non-leaf node, then k is dragged down to xi. and a key from s is pushed up to fill the place of k else k is simply replaced by a key in s return else merge xi with the sibling node s. Delete the corresponding child pointer in xi-1. if xi is an internal node, then drag the key in xi-1. which is previously divides xi and s. into the new node xi and s, into the new node xi. else delete that key in xi-1. i := i – 1 end if done
547 Views
