Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Binary Tree ADT in Data Structure
Basic concept
A binary tree is defined as a tree in which no node can have more than two children. The highest degree of any node is two. This indicates that the degree of a binary tree is either zero or one or two.
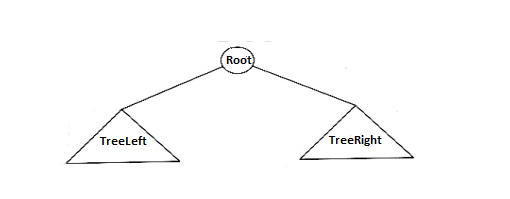
In the above fig., the binary tree consists of a root and two sub trees TreeLeft & TreeRight. All nodes to the left of the binary tree are denoted as left subtrees and all nodes to the right of a binary tree are referred to as right subtrees.
Implementation
A binary tree has maximum two children; we can assign direct pointers to them. The declaration of tree nodes is same as in structure to that for doubly linked lists, in that a node is a structure including the key information plus two pointers (left and right) to other nodes.
Binary Tree node declaration
typedef struct tree_node *tree_ptr;
struct tree_node
{
element_type element1;
tree_ptr left1; tree_ptr right1;
};
typedef tree_ptr TREE;Types of Binary Tree
Strictly binary tree
Strictly binary tree is defined as a binary tree where all the nodes will have either zero or two children. It does not include one child in any node.
Skew tree
A skew tree is defined as a binary tree in which every node except the leaf has only one child node. There are two types of skew tree, i.e. left skewed binary tree and right skewed binary tree.
Left skewed binary tree
A left skew tree has node associated with only the left child. It is a binary tree contains only left subtrees.
Right skewed binary tree
A right skew tree has node associated with only the right child. It is a binary tree contains only right subtrees.
Full binary tree or proper binary tree
A binary tree is defined as a full binary tree if all leaves are at the same level and every non leaf node has exactly two children and it should consist of highest possible number of nodes in all levels. A full binary tree of height h has maximum 2h+1 – 1 nodes.
Complete binary tree
Every non leaf node has exactly two children but all leaves are not necessary to belong at the same level. A complete binary tree is defined as one where all levels have the highest number of nodes except the last level. The last level elements should be filled from left to right direction.
Almost complete binary tree
An almost complete binary tree is defined as a tree in which each node that has a right child also has a left child. Having a left child does not need a node to have a right child
Differences between General Tree and Binary Tree
General Tree
- General tree has no limit of number of children.
- Evaluating any expression is hard in general trees.
Binary Tree
- A binary tree has maximum two children
- Evaluation of expression is simple in binary tree.
Application of trees
- Manipulation of arithmetic expression
- Construction of symbol table
- Analysis of Syntax
- Writing Grammar
- Creation of Expression Tree
6K+ Views
