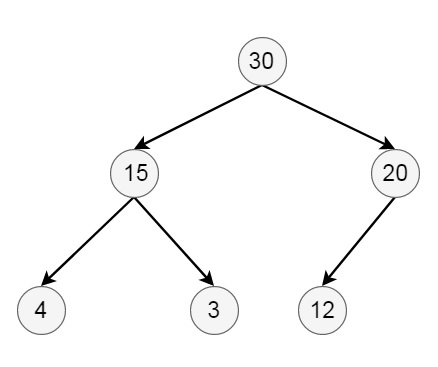
Deletion from a Max Heap in Data Structure

Here we will see how to delete elements from binary max heap data structures. Suppose the initial tree is like below −

Deletion Algorithm

delete(heap, n) −
Begin
   if heap is empty, then exit
   else
      item := heap[1]
      last := heap[n]
      n := n – 1
      for i := 1, j := 2, j <= n, set i := j and j := j * 2, do
         if j < n, then
            if heap[j] < heap[j + 1], then j := j + 1
         end if
         if last >= heap[j], then break
         heap[i] := heap[j]
      done
   end if
   heap[i] := last
End

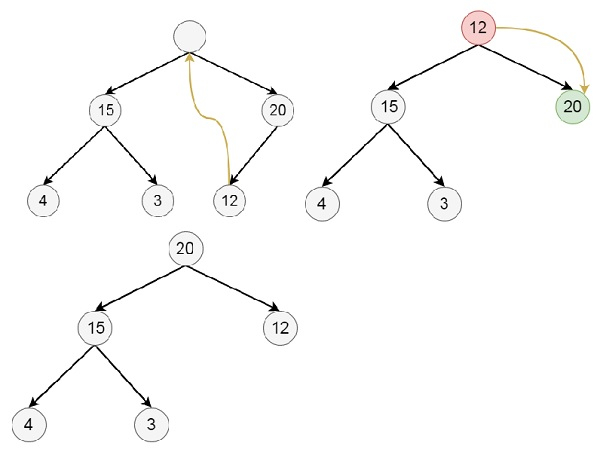
Example

Suppose we want to delete 30 from the final heap −

Arnab Chakraborty

Updated on: 10-Aug-2020

1K+ Views

Kickstart Your Career

Get certified by completing the course

Get Started