Splay in Virtual Tree in Data Structure
In virtual tree, some edges are treated as solid and some are treated as dashed. Usual splaying is performed only in the solid trees. To splay at a node y in the virtual tree, following method is implemented.
The algorithm looks at the tree three times, once in each pass, and changes it. In first pass, by splaying only in the solidtrees, beginning from the node y, the path from y to the root of the overall tree, becomes dashed. This path is createdsolid by splicing. A final splay at node y will now create y the root of the tree. Less informally, the algorithm is explained as follows
Algorithm for Splay(y)
Pass 1 Walk up the virtual tree, but splaying is performed only within solid sub-tree. At the end of this pass, the path from y to root becomes dashed.
Pass 2 Walk up from node y, splicing at each proper ancestor of y. At the end of this step, the path from y to the root becomes solid. Except that, the node y and all its children in the original tree (the one before pass 1) now become left children.
Pass 3 Walk up from node y to the root, splaying in the normal fashion.
This allows us to utilize prior knowledge to improve our probability estimations. For the given set of leaves. So the goal is to construct a tree with the minimum external path weight.
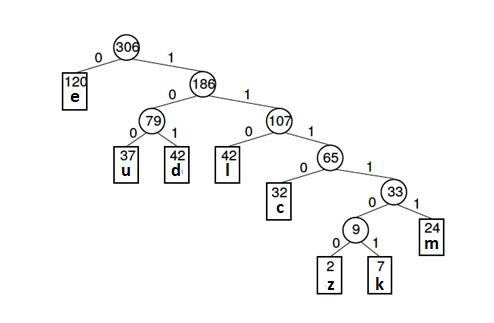
An example is given below
Letter frequency table
| Letter | z | k | m | c | u | d | l | e |
| Frequency | 2 | 7 | 24 | 32 | 37 | 42 | 42 | 120 |
Huffman code
| Letter | Freq | Code | Bits |
|---|
| e | 120 | 0 | 1 |
| d | 42 | 101 | 3 |
| l | 42 | 110 | 3 |
| u | 37 | 37
100 | 3 |
| c | 32 | 1110 | 4 |
| m | 24 | 11111 | 5 |
| k | 7 | 111101 | 6 |
| z | 2 | 111100 | 6 |
The Huffman tree (for above example) is given below
Published on 07-Jan-2020 12:17:26
