Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Binary Number System
Binary Number System is one the type of Number Representation techniques. It is most popular and used in digital systems. Binary system is used for representing binary quantities which can be represented by any device that has only two operating states or possible conditions. For example, a switch has only two states: open or close.
In the Binary System, there are only two symbols or possible digit values, i.e., 0 and 1. Represented by any device that only 2 operating states or possible conditions. Binary numbers are indicated by the addition of either an 0b prefix or an 2 suffix.
Position of every digit has a weight which is a power of 2. Each position in the Binary system is 2 times more significant than the previous position, that means numeric value of a Binary number is determined by multiplying each digit of the number by the value of the position in which the digit appears and then adding the products. So, it is also a positional (or weighted) number system.
| Most Significant Bit (MSB) | Binary Point | Least Significant Bit (LSB) | |||
|---|---|---|---|---|---|
| 22 | 21 | 20 | 2-1 | 2-2 | 2-3 |
| 4 | 2 | 1 | 0.5 | 0.25 | 0.125 |
Voltage range between 0V to 0.8V is used for binary logic 0 and voltage range between 2V to 5V is used for binary logic 1. Voltage range between 0.8V to 2V is not used because it may causes error in a digital circuit.
Example-1 − The number 125 is interpreted as
125 = 1x26+1x25+1x24+1x23+1x22+0x21+1x20=1111101
Here, right most bit 1 is the least significant bit (LSB) and left most bit 1 is the most significant bit (MSB).
Example-2 − The number 90.75 is interpreted as
90.75 = 1x26+0x25+1x24+1x23+0x22+1x21+0x20+1x2-1+1x2-2=1011010.11
Here, right most bit 1 is the least significant bit (LSB) and left most bit 1 is the most significant bit (MSB).
Example-3 − A decimal number 21 to represent in Binary representation
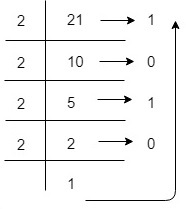
(21)10 =16+0+4+0+1 = 1x24+0x23+1x22+0x21+1x20 =(10101)2 So, decimal value 21 is equivalent to 10101 in Binary Number System.
Applications of Binary Number System
The binary number system is very useful in computer technology and computer programming languages also uses binary number system that is helpful in digital encoding. The binary number system can also be used in Boolean algebra.
Advantages and Disadvantages
The main advantage of using binary is that it is a base which is easily represented by electronic devices. The Binary Number System are also ease of use in coding, fewer computations and less computational errors.
The major disadvantage of binary number is difficult to read and write for humans because of large number of binary of a equivalent decimal number.
1’s and 2’s Complement of Binary (Base-2) Number
To get 1’s complement of a binary number, simply invert the given number. For example, 1’s complement of binary number 110010 is 001101.
2’s complement of binary number is 1’s complement of given number plus 1 to the least significant bit (LSB). For example 2’s complement of binary number 10010 is (01101) + 1 = 01110.
6K+ Views
