Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Octal Number System
Octal Number System is one the type of Number Representation techniques, in which there value of base is 8. That means there are only 8 symbols or possible digit values, there are 0, 1, 2, 3, 4, 5, 6, 7. It requires only 3 bits to represent value of any digit. Octal numbers are indicated by the addition of either an 0o prefix or an 8 suffix.
Position of every digit has a weight which is a power of 8. Each position in the Octal system is 8 times more significant than the previous position, that means numeric value of an octal number is determined by multiplying each digit of the number by the value of the position in which the digit appears and then adding the products. So, it is also a positional (or weighted) number system.
Representation of Octal Number
Each Octal number can be represented using only 3 bits, with each group of bits having a distich values between 000 (for 0) and 111 (for 7 = 4+2+1). The equivalent binary number of Octal number are as given below −
| Octal Digit Value | Binary Equivalent |
|---|---|
| 0 | 000 |
| 1 | 001 |
| 2 | 010 |
| 3 | 011 |
| 4 | 100 |
| 5 | 101 |
| 6 | 110 |
| 7 | 111 |
Octal number system is similar to Hexadecimal number system. Octal number system provides convenient way of converting large binary numbers into more compact and smaller groups, however this octal number system is less popular.
| Most Significant Bit (MSB) | Octal Point | Least Significant Bit (LSB) | |||
|---|---|---|---|---|---|
| 82 | 81 | 80 | 8-1 | 8-2 | 8-3 |
| 64 | 8 | 1 | 1/8 | 1/64 | 1/512 |
Since base value of Octal number system is 8, so there maximum value of digit is 7 and it can not be more than 7. In this number system, the successive positions to the left of the octal point having weights of 80, 81, 82, 83 and so on. Similarly, the successive positions to the right of the octal point having weights of 8-1, 8-2, 8-3and so on. This is called base power of 8. The decimal value of any octal number can be determined using sum of product of each digit with its positional value.
Example-1 − The number 111 is interpreted as
111 = 1x82+5x81+7x80 = 157
Here, right most bit 7 is the least significant bit (LSB) and left most bit 1 is the most significant bit (MSB).
Example-2 − The number 65.125 is interpreted as
65.125 =1x82+0x81+1x80+1x8-1=101.10
Here, right most bit 0 is the least significant bit (LSB) and left most bit 1 is the most significant bit (MSB).
Example-3 − A decimal number 21 to represent in Octal representation
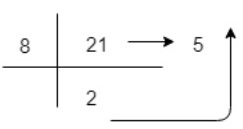
(21)10=2x81+5x80=(25)8 So, decimal value 21 is equivalent to 25 in Octal Number System.
Applications of Octal Number System
The octal numbers are not as common as they used to be. However, Octal is used when the number of bits in one word is a multiple of 3. It is also used as a shorthand for representing file permissions on UNIX systems and representation of UTF8 numbers, etc.
Advantages and Disadvantages
The main advantage of using Octal numbers is that it uses less digits than decimal and Hexadecimal number system. So, it has fewer computations and less computational errors. It uses only 3 bits to represent any digit in binary and easy to convert from octal to binary and vice-versa. It is easier to handle input and output in the octal form.
The major disadvantage of Octal number system is that computer does not understand octal number system directly, so we need octal to binary converter.
7’s and 8’s Complement of Octal (Base-8) Number
Simply, 7’s complement of a octal number is the subtraction of it’s each digits from 7. For example, 7’s complement of octal number 127 is 777 - 127 = 650.
8’s complement of octal number is 7’s complement of given number plus 1 to the least significant bit (LSB). For example 8’s complement of octal number 320 is (777 - 320) + 1 = 457 + 1 = 460. Please note that maximum digit of octal number system is 7, so addition of 7+1 will be 0 with carry 1.
11K+ Views
