Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Negative Binary Numbers
Negative numbers can be distinguishable with the help of extra bit or flag called sign bit or sign flag in Binary number representation system for signed numbers. It is not possible to add minus or plus symbol in front of a binary number because a binary number can have only two symbol either 0 or 1 for each position or bit. That’s why we use this extra bit called sign bit or sign flag. The value of sign bit is 1 for negative binary numbers and 0 for positive numbers.
When an integer binary number is positive, the sign is represented by 0 and the magnitude by a positive binary number. When the number is negative, the sign is represented by 1 but the rest of the number may be represented in one of three possible ways: Sign-Magnitude method, 1’s Complement method, and 2’s complement method. These are explained as following below.
1. Signed Magnitude Method:
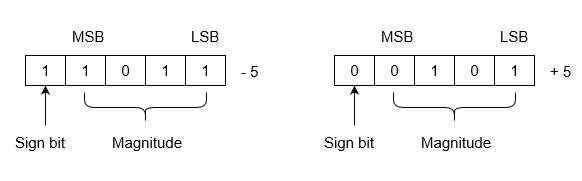
In this method, number is divided into two parts: Sign bit and Magnitude. If the number is positive then sign bit will be 0 and if number is negative then sign bit will be 1. Magnitude is represented with the binary form of the number to be represented.
Example: Let we are using 5 bits register. The representation of -5 to +5 will be as follows:
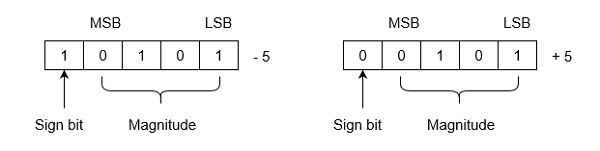
Range of Numbers: For k bits register, MSB will be sign bit and (k-1) bits will be magnitude. Positive largest number that can be stored is (2(k-1)-1) and negative lowest number that can be stored is -(2(k-1)-1).
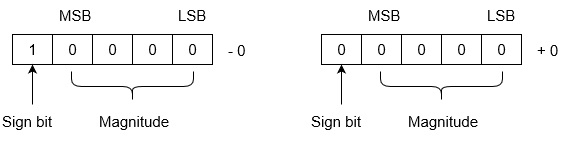
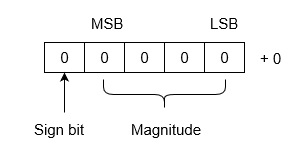
Note that drawback of this system is that 0 has two different representation one is -0 (e.g., 1 0000 in five bit register) and second is +0 (e.g., 0 0000 in five bit register).
2. 1’s Complement Method:
Positive numbers are represented in the same way as they are represented in sign magnitude method. If the number is negative then it is represented using 1’s complement. First represent the number with positive sign and then take 1’s complement of that number.
Example: Let we are using 5 bits register. The representation of -5 and +5 will be as follows:
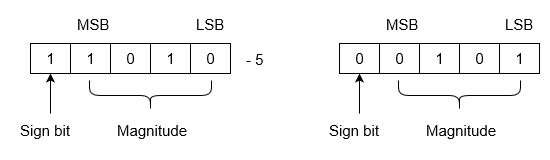
+5 is represented as it is represented in sign magnitude method. -5 is represented using the following steps:
(i) +5 = 0 0101
(ii) Take 1’s complement of 0 0101 and that is 1 1010. MSB is 1 which indicates that number is negative.
MSB is always 1 in case of negative numbers.
Range of Numbers: For k bits register, positive largest number that can be stored is (2(k-1)-1) and negative lowest number that can be stored is -(2(k-1)-1).
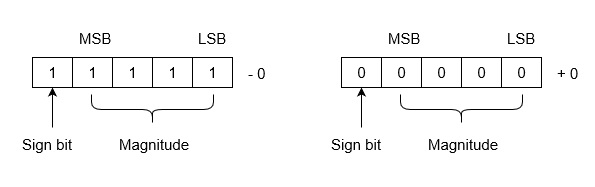
Note that drawback of this system is that 0 has two different representation one is -0 (e.g., 1 1111 in five bit register) and second is +0 (e.g., 0 0000 in five bit register).
3. 2’s Complement Method: Positive numbers are represented in the same way as they are represented in sign magnitude method. If the number is negative then it is represented using 2’s complement. First represent the number with positive sign and then take 2’s complement of that number.
Example: Let we are using 5 bits registers. The representation of -5 and +5 will be as follows:
+5 is represented as it is represented in sign magnitude method. -5 is represented using the following steps:
(i) +5 = 0 0101
(ii) Take 2’s complement of 0 0101 and that is 1 1011. MSB is 1 which indicates that number is negative.
MSB is always 1 in case of negative numbers.
Range of Numbers: For k bits register, positive largest number that can be stored is (2(k-1)-1) and negative lowest number that can be stored is -(2(k-1)).
The advantage of this system is that 0 has only one representation for -0 and +0. Zero (0) is considered as always positive (sign bit is 0) in 2’s complement representation. Therefore, it is unique or unambiguous representation.
These are representation method for signed binary numbers.
13K+ Views
