Biggest Reuleaux Triangle inscribed within a Square inscribed in an equilateral triangle in C?

A Reuleaux triangle is a shape formed from the intersection of three circular disks, each having its center on the boundary of the other two. Its boundary is a curve of constant width, the simplest and best known such curve other than the circle itself. Constant width means that the separation of every two parallel supporting lines is the same, independent of their orientation. Because all its diameters are the same.

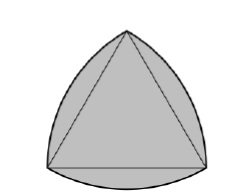
The boundary of a Reuleaux triangle is a constant width curve based on an equilateral triangle. All points on a side are equidistant from the opposite vertex.

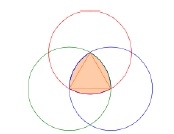
To construct a Reuleaux triangle

Formula for Reuleaux triangle

Area of the Reuleaux Triangle, if curve based on an equilateral triangle and side of triangle is h

A = (π * h2) / 2 – 2 * (Area of equilateral triangle) = (π – √3) * h2 / 2 = 0.70477 * h2

Biggest Reuleaux Triangle inscribed within a Square inscribed in an equilateral triangle

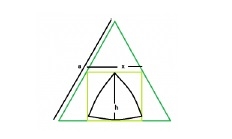
Biggest Reuleaux Triangle inscribed within a Square inscribed in an equilateral triangle

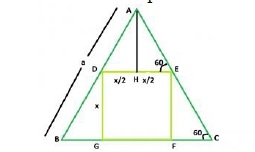
Biggest Square that can be inscribed within an Equilateral triangle

the side of the square be x.

a = 2x/√3 + x

x = a/(1 + 2/√3) = 0.464a

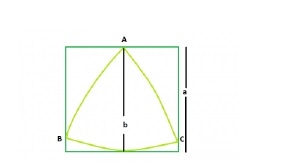
Biggest Reuleaux Triangle within A Square

Area of Reuleaux Triangle is 0.70477 * b² where b is the distance between the parallel lines supporting the Reuleaux Triangle.

distance between parallel lines supporting the Reuleaux Triangle = Side of the square i.e. a

Area of the Reuleaux Triangle, A = 0.70477 * a²

Let’s take an example,

Input: 5
Output: 3.79335

Explanation

Given here is an equilateral triangle of side length a which inscribes a square which in turn inscribes a reuleaux triangle. The task is to find the maximum possible area of this reuleaux triangle.

the side of the square inscribed within an equilateral triangle of side length a is, x = 0.464*a 

in the reuleaux triangle, h = x.

Area of Reuleaux Triangle:

A = 0.70477*h²

= 0.70477*(0.464*a)²

Example

#include <stdio.h>
#include <math.h>
int main() {
   float a = 3;
   float x = 0.464 * a;
   float area = 0.70477 * pow(x, 2);
   printf("The area is %f", area);
   return 0;
}

Output

The area is 1.365607