Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Biggest Reuleaux Triangle inscribed within a Square inscribed in an equilateral triangle?
Here we will see the area of biggest Reuleax triangle inscribed within a square which is inscribed in an equilateral triangle. Suppose ‘a’ is the side of the triangle. The side of the square is x and the height of the Reuleaux triangle is h.
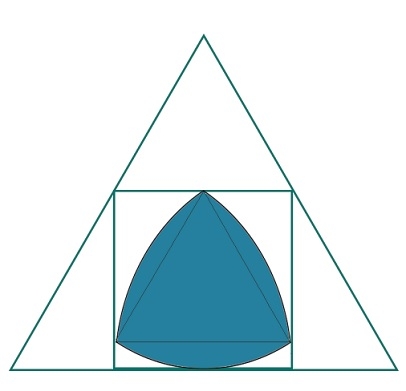
The side of the triangle is −
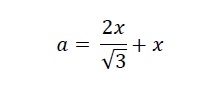
So the value of x is −
𝑥 = 0.464𝑎
The height of the Reuleaux triangle is the same as x. So x = h. So the area of the Reuleaux triangle is −
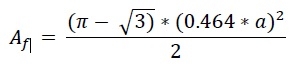
Example
#include <iostream>
#include <cmath>
using namespace std;
float areaReuleaux(float a) { //side of triangle is a
if (a < 0) //if a is negative it is invalid
return -1;
float area = ((3.1415 - sqrt(3)) * (0.464*a) * (0.464*a))/2;
return area;
}
int main() {
float side = 5;
cout << "Area of Reuleaux Triangle: " << areaReuleaux(side);
}Output
Area of Reuleaux Triangle: 3.79311
Updated on: 01-Aug-2019
54 Views
Advertisements