Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
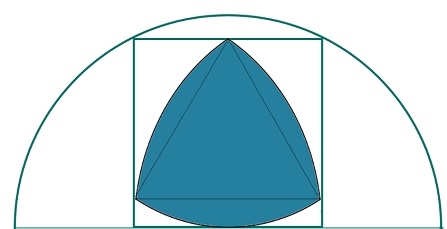
Biggest Reuleaux Triangle inscirbed within a square inscribed in a semicircle?
Here we will see the area of biggest Reuleax triangle inscribed within a square which is inscribed in a semicircle. Suppose the radius of the semicircle is R, are side of the square is ‘a’ and the height of the Reuleax triangle is h.
We know that the side of the square inscribed in a semicircle is −
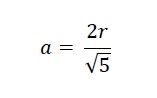
The height of the Reuleaux triangle is the same as a. So a = h. So the area of the Reuleaux triangle is −
Example
#include <iostream>
#include <cmath>
using namespace std;
float areaReuleaux(float r) { //radius of the semicircle is r
if (r < 0) //if r is negative it is invalid
return -1;
float area = ((3.1415 - sqrt(3)) * (2*r/(sqrt(5))) * (2*r/(sqrt(5))))/2;
return area;
}
int main() {
float rad = 8;
cout << "Area of Reuleaux Triangle: " << areaReuleaux(rad);
}Output
Area of Reuleaux Triangle: 36.0819
Updated on: 01-Aug-2019
52 Views
Advertisements