Biggest Reuleaux Triangle within a Square which is inscribed within a Right angle Triangle in C?

A Reuleaux triangle is a shape formed from the intersection of three circular disks, each having its center on the boundary of the other two. Its boundary is a curve of constant width, the simplest and best known such curve other than the circle itself. Constant width means that the separation of every two parallel supporting lines is the same, independent of their orientation. Because all its diameters are the same.

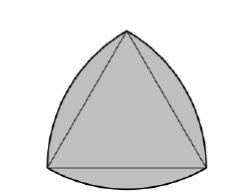
The boundary of a Reuleaux triangle is a constant width curve based on an equilateral triangle. All points on a side are equidistant from the opposite vertex.

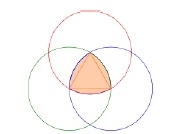
To construct a Reuleaux triangle

Formula for Reuleaux triangle

Area of the Reuleaux Triangle, if curve based on an equilateral triangle and side of triangle is h

A = (π * h2) / 2 – 2 * (Area of equilateral triangle) = (π – √3) * h2 / 2 = 0.70477 * h2

Biggest Reuleaux Triangle within a Square which is inscribed within a Right angle Triangle

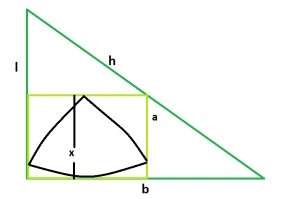
Biggest Reuleaux Triangle within a Square which is inscribed within a Right angle Triangle

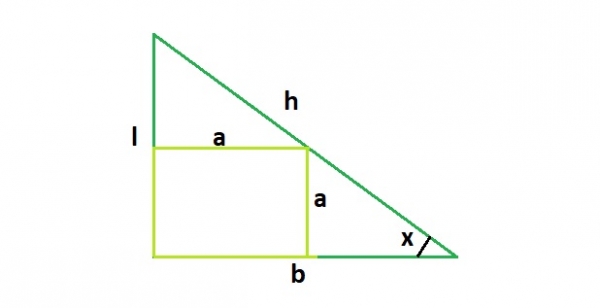
from the above diagram, a = (l*b)/(l+b)

Biggest Reuleaux Triangle within A Square

Area of Reuleaux Triangle is 0.70477 * b² where b is the distance between the parallel lines supporting the Reuleaux Triangle.

distance between parallel lines supporting the Reuleaux Triangle = Side of the square i.e. a

Area of the Reuleaux Triangle, A = 0.70477 * a²

Let’s take an example to illustrate the concept,

Input: l = 3, b = 4, h = 5
Output: 2.07116

Explanation

The side of the square inscribed within a right angled triangle is, a = (l*b)/(l+b),

in the reuleaux triangle, x = a.

x = (l*b)/(l+b).

Area of the Reuleaux Triangle is, A = 0.70477*x^2 = 0.70477*((l*b)/(l+b))^2.

Example

#include <stdio.h>
#include<math.h>
int main() {
   float l = 3,b = 4;
   float x = (l * b) / (l + b);
   float area = 0.70477 * pow(x, 2);
   printf("The area is : %f", area);
   return 0;
}

Output

The area is : 2.071161