Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Biggest Reuleaux Triangle within a Square which is inscribed within a Circle?
Here we will see the area of biggest Reuleaux triangle inscribed within a square, That square is inscribed inside one circle. The side of the square is ‘a’. The radius of the circle is ‘r’. As we know that the diagonal of the square is the diameter of the circle. So −
2𝑟 = 𝑎√2 𝑎 = 𝑟√2
And the height of the Reuleaux triangle is h.
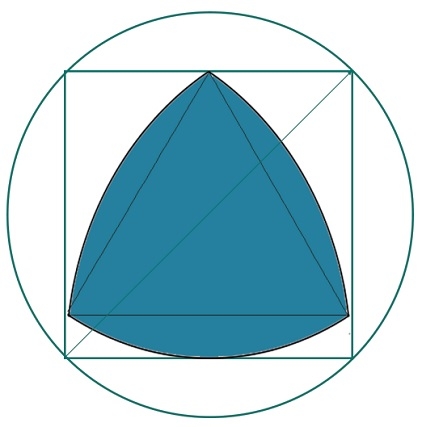
The height of the Reuleaux triangle is same as a. So a = h. So the area of Reuleaux triangle is −
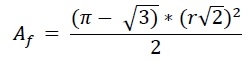
Example
#include <iostream>
#include <cmath>
using namespace std;
float areaReuleaux(float r) { //radius of ciecle is r
if (r < 0) //if a is negative it is invalid
return -1;
float area = ((3.1415 - sqrt(3)) * (r * sqrt(2)) * (r * sqrt(2)))/2;
return area;
}
int main() {
float rad = 6;
cout << "Area of Reuleaux Triangle: " << areaReuleaux(rad);
}Output
Area of Reuleaux Triangle: 50.7402
Updated on: 01-Aug-2019
58 Views
Advertisements