Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Wireless Channel Noise: Solved Problems on Noise Power
In this section, we will solve some problems on wireless channel noise based on the white noise model.
Example Problem 1
A white noise has a 2-sided power spectral density of 6 kW/MHz. It is passed through a low pass filter having a bandwidth of 1 kHz. Compute the output noise power.
Solution −
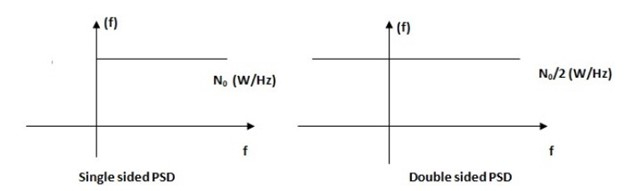
The 2-sided power spectral density is 6 kW/MHz. The power spectral density is usually represented in W/Hz.
$$\frac{6kW}{MHz}=\frac{6000W}{1000000Hz}=\frac{0.006W}{Hz}=\frac{N_{0}}{2}$$
The 2-sided power spectral density N0/2 is 0.006W/Hz. Therefore, N0 = 0.012W/Hz.
The noise power is expressed as the product of the noise power spectral density and the noise bandwidth.
$$N_{p}=N_{0}.BW$$
$$N_{p}=\frac{0.012W}{Hz}.1kHz=12W$$
The noise power of the given system is 12W
Example Problem 2
A composite TV signal has a bandwidth of 40 MHz and is transmitted with a power of 0.1 W through a satellite channel. The white noise has a 2 sided PSD is 10-15 W/Hz. What is the noise power for the link?
Solution − The noise power is expressed as the product of the system bandwidth and the noise power spectral density. The noise is going to exist over the range of the frequencies over which the signal is going to be transmitted. Hence, the signal bandwidth is equal to the noise bandwidth.
The one-sided PSD of noise can be found using the data given.
$$\frac{N_{0}}{2}=10^{-15}\frac{W}{Hz}\Rightarrow\:N_{0}=2\times\:10^{-15}W/Hz$$
Using the values given, we find that the noise power is
$$(40\times\:10^{6}).(2\times\:10^{-15})W=80nW$$
Example Problem 3
The noise level available at the output of a communication receiver is -10 dBm. What is the noise level in the absolute scale?
Solution − The noise power in absolute scale is computed as follows −
$$10log_{10}(\frac{N_{p}}{1mW})=-10dBm$$
$$log_{10}(\frac{N_{p}}{1mW})=-1\Rightarrow\:\frac{N_{p}}{1mW}=10^{-1}$$
$$N_{p}=10^{-1}mW=100\mu\:W$$
Therefore, the noise power is found out to be 100 microwatts
729 Views
