Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
What is the Volume of Conductor Material Required in Underground DC System?
Underground DC System
When the DC electric power is transmitted from the power generating station to the consumer through the underground cables, then the electric power transmission system is called the underground DC system.
The underground DC transmission system is classified into three types −
Two-Wire DC System
Two-Wire DC System with Mid-Point Earthed
Three-Wire DC System
Conductor Material Required in Underground 2-Wire DC System
The underground two-wire DC system is shown in Figure-1. It has two conductors taken from the generator terminals.
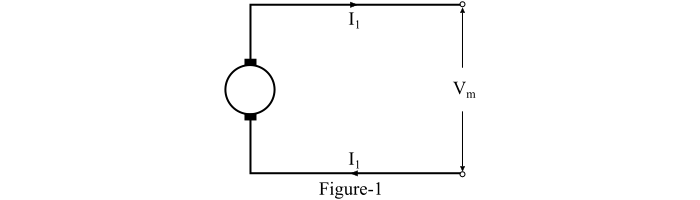
Let,
𝑉𝑚 = Maximum voltage between conductors
𝑃 = Power to be transmitted
𝑙 = Distance for which power is transmitted
The load current is given by,
$$\mathrm{\mathit{I_{\mathrm{1}}\mathrm{\, =\, }\frac{P}{V_{m}}}}$$
If 𝑎1 is the cross-sectional area of each conductor, then the resistance per conductor is,
$$\mathrm{\mathit{R_{\mathrm{1}}\mathrm{\, =\, }\rho \frac{l}{a_{\mathrm{1}}}}}$$
The total power losses in the system are given by,
$$\mathrm{\mathit{W\mathrm{\, =\, }\mathrm{2}I\mathrm{_{1}^{2}}\, R_{\mathrm{1}}\mathrm{\, =\, }\mathrm{2}\times \left ( \frac{P}{V_{m}} \right )^{\mathrm{2}}\times \left ( \frac{\rho \, l}{a_{\mathrm{1}}} \right )}}$$
$$\mathrm{\mathit{\Rightarrow W\mathrm{\, =\, }\frac{\mathrm{2}P^{\mathrm{2}\, }\rho l}{V_{m}^{\mathrm{2}}a_{\mathrm{1}}} }}$$
$$\mathrm{\therefore Area\: of\: cross\: section,\mathit{ \: a_{\mathrm{1}}\mathrm{\, =\, }\frac{\mathrm{2}P^{\mathrm{2}\, }\rho l}{WV_{m}^{\mathrm{2}}} }}$$
Thus, the volume of conductor material required in the underground 2-wire DC system, say K, is given by,
$$\mathrm{\mathit{ K\mathrm{\, =\, }\mathrm{2}a_{\mathrm{1}}l\mathrm{\, =\, }\mathrm{2}\times \left ( \frac{\mathrm{2}P^{\mathrm{2}\, }\rho l}{WV_{m}^{\mathrm{2}}} \right )\times l}}$$
$$\mathrm{\mathit{\therefore K\mathrm{\, =\, }\frac{\mathrm{4}P^{\mathrm{2}\, }\rho l^{\mathrm{2}}}{WV_{m}^{\mathrm{2}}}}\: \: \: \cdot \cdot \cdot \left ( 1 \right )} $$
Conductor Material Required in Underground 2-Wire DC System with Mid-Point Earthed
The circuit diagram of the underground 2-wire DC system with mid-point earthed is shown in Figure-2.
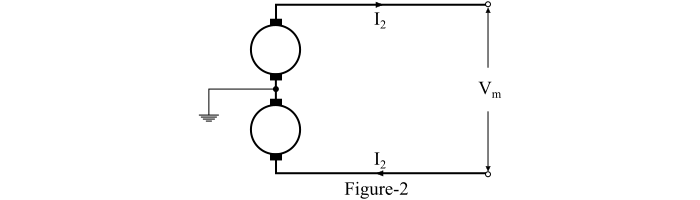
Let,
- 𝑉𝑚 = Maximum voltage between conductors
- 𝑃 = Power to be transmitted
Then, the load current is given by,
$$\mathrm{\mathit{I_{\mathrm{2}}\mathrm{\, =\, }\frac{P}{V_{m}}}}$$
If 𝑎2 is the area of cross-section of each conductor, then the resistance per conductor is,
$$\mathrm{\mathit{R_{\mathrm{2}}\mathrm{\, =\, }\rho \frac{l}{a_{\mathrm{2}}}}}$$
The total power losses in the system is given by,
$$\mathrm{\mathit{W\mathrm{\, =\, }\mathrm{2}I\mathrm{_{2}^{2}}\, R_{\mathrm{2}}\mathrm{\, =\, }\mathrm{2}\times \left ( \frac{P}{V_{m}} \right )^{\mathrm{2}}\times \left ( \frac{\rho \, l}{a_{\mathrm{2}}} \right )}}$$
$$\mathrm{\mathit{\Rightarrow W\mathrm{\, =\, }\frac{\mathrm{2}P^{\mathrm{2}\, }\rho l}{V_{m}^{\mathrm{2}}a_{\mathrm{2}}} }}$$
$$\mathrm{\therefore Area\: of\: cross\: section,\mathit{ \: a_{\mathrm{2}}\mathrm{\, =\, }\frac{\mathrm{2}P^{\mathrm{2}\, }\rho l}{WV_{m}^{\mathrm{2}}} }} $$
Therefore, the volume of conductor material required in the underground 2-wire DC system with mid-point earthed, say K1, is given by,
$$\mathrm{\mathit{ K_{\mathrm{1}}\mathrm{\, =\, }\mathrm{2}a_{\mathrm{2}}l\mathrm{\, =\, }\mathrm{2}\times \left ( \frac{\mathrm{2}P^{\mathrm{2}\, }\rho l}{WV_{m}^{\mathrm{2}}} \right )\times l}}$$
$$\mathrm{\mathit{\therefore K_{\mathrm{1}}\mathrm{\, =\, }\frac{\mathrm{4}P^{\mathrm{2}\, }\rho l^{\mathrm{2}}}{WV_{m}^{\mathrm{2}}}}\: \: \: \cdot \cdot \cdot \left ( 2 \right )}$$
Comparing equations (1) & (2), we get,
$$\mathrm{\mathit{\frac{K_{\mathrm{1}}}{K}\mathrm{\, =\, }\frac{\left ( \frac{\mathrm{4}P^{\mathrm{2}\, }\rho l^{\mathrm{2}}}{WV_{m}^{\mathrm{2}}} \right )}{\left (\frac{\mathrm{4}P^{\mathrm{2}\, }\rho l^{\mathrm{2}}}{WV_{m}^{\mathrm{2}}} \right )}}\mathrm{\, =\, }1}$$
$$\mathrm{\mathit{\therefore K_{\mathrm{1}}\mathrm{\, =\, }K}\: \: \: \cdot \cdot \cdot \left ( 3 \right )} $$
Hence, the volume of conductor material required in the underground 2-wire DC system with mid-point earthed is the same as that for underground 2-wire DC system.
Conductor Material Required in Underground Three-Wire DC System
The circuit diagram of an underground three-wire DC system is shown in Figure-3. In this system, the two outer line conductors are taken from the outer terminals of the generators and the neutral wire is taken from the mid-point. When the balanced load is connected to the system, the current in the neutral wire will be zero.
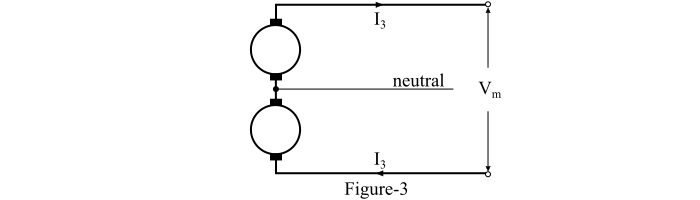
Let,
𝑉𝑚 = Maximum voltage between outer conductors
𝑃 = Power to be transmitted
Then, the load current in the system is given by,
$$\mathrm{\mathit{I_{\mathrm{3}}\mathrm{\, =\, }\frac{P}{V_{m}}}}$$
Also, if 𝑎3 is the area of cross-section of each conductor, then the resistance per conductor is,
$$\mathrm{\mathit{R_{\mathrm{3}}\mathrm{\, =\, }\rho \frac{l}{a_{\mathrm{3}}}}}$$
Hence, the total power losses in the system are given by,
$$\mathrm{\mathit{W\mathrm{\, =\, }\mathrm{2}I\mathrm{_{3}^{2}}\, R_{\mathrm{3}}\mathrm{\, =\, }\mathrm{2}\times \left ( \frac{P}{V_{m}} \right )^{\mathrm{2}}\times \left (\rho \frac{ \, l}{a_{\mathrm{3}}} \right )}}$$
$$\mathrm{\mathit{\Rightarrow W\mathrm{\, =\, }\frac{\mathrm{2}P^{\mathrm{2}\, }\rho l}{V_{m}^{\mathrm{2}}a_{\mathrm{3}}} }}$$
$$\mathrm{\therefore Area\: of\: cross\: section,\mathit{ \: a_{\mathrm{3}}\mathrm{\, =\, }\frac{\mathrm{2}P^{\mathrm{2}\, }\rho l}{WV_{m}^{\mathrm{2}}} }}$$
Assuming the area of cross-section of the neutral wire to be half of that of outer line wires.
Therefore, the volume of conductor material required in the underground three-wire DC system, say K2, is given by,
$$\mathrm{\mathit{ K_{\mathrm{2}}\mathrm{\, =\, }\mathrm{2.5}a_{\mathrm{3}}l\mathrm{\, =\, }\mathrm{2.5}\times \left ( \frac{\mathrm{2}P^{\mathrm{2}\, }\rho l}{WV_{m}^{\mathrm{2}}} \right )\times l}}$$
$$\mathrm{\mathit{\therefore K_{\mathrm{2}}\mathrm{\, =\, }\frac{\mathrm{5}P^{\mathrm{2}\, }\rho l^{\mathrm{2}}}{WV_{m}^{\mathrm{2}}}}\: \: \: \cdot \cdot \cdot \left ( 4 \right )}$$
Comparing equation (4) with (1), we get,
$$\mathrm{\mathit{ \frac{K_{\mathrm{2}}}{K}\mathrm{\, =\, }\frac{\left ( \frac{\mathrm{5}P^{\mathrm{2}\, }\rho l^{\mathrm{2}}}{WV_{m}^{\mathrm{2}}} \right )}{\left ( \frac{\mathrm{4}P^{\mathrm{2}\, }\rho l^{\mathrm{2}}}{WV_{m}^{\mathrm{2}}} \right )}}\mathrm{\, =\, }1.25}$$
$$\mathrm{\mathit{\therefore K_{\mathrm{2}}\mathrm{\, =\, }\mathrm{1.25}\times K}\: \: \: \cdot \cdot \cdot \left ( 5 \right )}$$
Hence, the volume of conductor material require in the underground three-wire DC system is 1.25 times that required for the underground 2-wire DC system.
402 Views
