Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Conductor Material Required in Three-Phase Overhead AC Transmission System
Three-Phase Transmission System
A three-phase transmission system is the one in which three line conductors are used to transmit the AC electric power from generating station to the substations. The three-phase system is universally adopted for transmission of electric power.
Depending upon the number of conductors used, the three-phase AC transmission system is classified into two types viz. −
- Three-Phase Three-Wire System
- Three-Phase Four-Wire System
Conductor Material Required in 3-Phase 3-Wire AC System
Consider a three-phase three-wire AC system as shown in Figure-1, it has three line conductors and one earthed neutral wire. The three-phase three-wire system may be star connected (as shown in Figure-1) or delta connected.
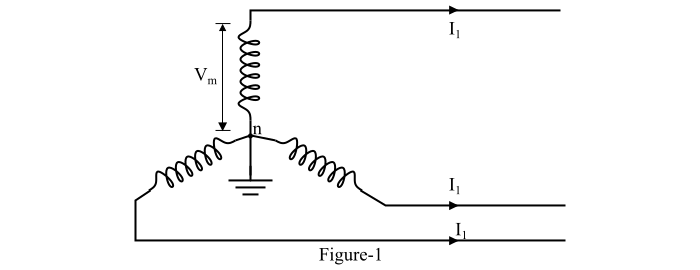
Let,
$\mathrm{Maximum \: voltage\: per\: phase,\: \mathit{V_{ph}\mathrm{\, =\, }V_{m}}}$
$\mathrm{RMS\: value\: of\: voltage\: per\: phase\: \mathit{\mathrm{\, =\, }\frac{V_{m}}{\mathrm{\sqrt{2}}}}}$
$\mathrm{Power\: transmitted\: by\: per\: phase\: \mathit{\mathrm{\, =\, }\frac{P}{\mathrm{3}}}}$
Therefore, the load current per phase is given by,
$$\mathrm{\mathit{I_{\mathrm{1}}\mathrm{\, =\, }\frac{P/\mathrm{3}}{\left ( \frac{V_{m}}{\sqrt{\mathrm{2}}}\mathrm{cos}\, \phi \right )}\mathrm{\, =\, }\frac{\sqrt{\mathrm{2}}P}{\mathrm{3}V_{m}\, \mathrm{cos}\, \phi} } }$$
If 𝑎1 is the area of cross-section of each conductor, then the resistance per conductor is given by,
$$\mathrm{\mathit{R_{\mathrm{1}}\mathrm{\, =\, }\frac{\rho \, l}{a_{\mathrm{1}}}}}$$
Hence, the total power losses in the transmission line are
$$\mathrm{\mathit{W\mathrm{\, =\, }\mathrm{3}I\mathrm{_{1}^{2}}\, R_{\mathrm{1}}\mathrm{\, =\, }\mathrm{3}\times \left ( \frac{\mathrm{\sqrt{2}}P}{\mathrm{3}V_{m}\mathrm{cos}\, \phi } \right )^{\mathrm{2}}\times \left ( \frac{\rho \, l}{a_{\mathrm{1}}} \right )\mathrm{\, =\, }\frac{\mathrm{2}P^{\mathrm{2}\, }\rho l}{\mathrm{3}V_{m}^{\mathrm{2}}\,\mathrm{cos^{2}\phi \,a_{\mathrm{1}}} }}}$$
$$\mathrm{\therefore Area\: of\: cross\: section,\mathit{ a_{\mathrm{1}}\mathrm{\, =\, }\frac{\mathrm{2}P^{\mathrm{2}\, }\rho l}{\mathrm{3}WV_{m}^{\mathrm{2}}\,\mathrm{cos^{2}\phi }\, }}}$$
Therefore, the volume (say K) of conductor material required in the three-phase three wire overhead AC transmission system is given by,
$$\mathrm{\mathit{K\mathrm{\, =\, }\mathrm{3}\times a_{\mathrm{1}}\times l\mathrm{\, =\, }\mathrm{3}\times \frac{\mathrm{2}P^{\mathrm{2}\, }\rho l}{\mathrm{3}WV_{m}^{\mathrm{2}}\,\mathrm{cos^{2}\phi }\, }\times l}}$$
$$\mathrm{\mathit{\therefore K\mathrm{\, =\, }\frac{\mathrm{2}P^{\mathrm{2}\, }\rho l^{\mathrm{2}}}{WV_{m}^{\mathrm{2}}\,\mathrm{cos^{2}\phi }\, }}\, \, \, \cdot \cdot \cdot \left ( 1 \right )}$$
Conductor Material Required in 3-Phase 4-Wire AC System
The three-phase four-wire AC transmission system is shown in Figure-2. In this system, the neutral wire is taken from the neutral point and the cross-sectional are of neutral wire is generally one-half that of the line conductors.
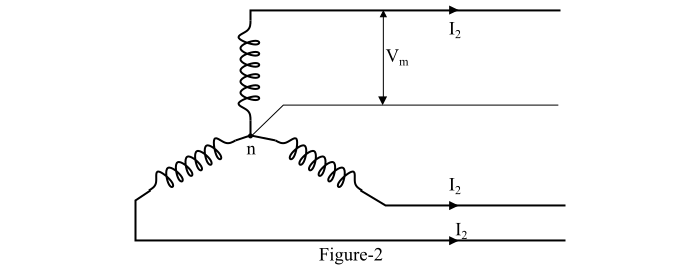
If the load connected to the 3-phase 4-wire system is balanced, then current through the neutral wire is zero.
Let,
$\mathrm{Maximum \: voltage\: per\: phase,\: \mathit{V_{ph}\mathrm{\, =\, }V_{m}}}$
$\mathrm{RMS\: value\: of\: voltage\: per\: phase\: \mathit{\mathrm{\, =\, }\frac{V_{m}}{\mathrm{\sqrt{2}}}}}$
$\mathrm{Power\: transmitted\: by\: per\: phase\: \mathit{\mathrm{\, =\, }\frac{P}{\mathrm{3}}}}$
Also, assume that the load is balanced and power factor of load as cos𝜙. Then,
$$\mathrm{Per\: phase\: load \: current,\: \mathit{I_{\mathrm{2}}\mathrm{\, =\, }\frac{P/\mathrm{3}}{\left ( \frac{V_{m}}{\sqrt{\mathrm{2}}}\mathrm{cos}\, \phi \right )}\mathrm{\, =\, }\frac{\sqrt{\mathrm{2}}P}{\mathrm{3}V_{m}\, \mathrm{cos}\, \phi} } }$$
If a2 is the area of cross-section of each line conductor and 𝑎𝑛=(𝑎2/2) is the cross-sectional area of neutral wire. Then
$$\mathrm{Resistance\: of\: each\: line \: conductor,\: \mathit{R_{\mathrm{2}}\mathrm{\, =\, }\frac{\rho \, l}{a_{\mathrm{2}}}}}$$
And,
$$\mathrm{Resistance\: of\: neutral\: wire,\: \mathit{R_{n}\mathrm{\, =\, }\frac{\rho \, l}{a_{n}}\mathrm{\, =\, }\frac{\mathrm{2}\rho \, l}{a_{\mathrm{2}}}}}$$
Since when a balanced three phase load is connected to the system, the neutral current is zero and hence no power loss in the neutral wire.
$$\mathrm{\therefore Line \: losses\:\mathit{ W\mathrm{\, =\, }\mathrm{3}I\mathrm{_{2}^{2}}\, R_{\mathrm{2}}\mathrm{\, =\, }\mathrm{3}\times \left ( \frac{\mathrm{\sqrt{2}}P}{\mathrm{3}V_{m}\mathrm{cos}\, \phi } \right )^{\mathrm{2}}\times \left ( \frac{\rho \, l}{a_{\mathrm{2}}} \right )}}$$
$$\mathrm{\mathit{\Rightarrow W\mathrm{\, =\, }\frac{\mathrm{2}P^{\mathrm{2}\, }\rho l}{\mathrm{3}V_{m}^{\mathrm{2}}\,\mathrm{cos^{2}\phi \,a_{\mathrm{2}}} }}}$$
$$\mathrm{\therefore Area\: of\: cross\: section,\mathit{ a_{\mathrm{2}}\mathrm{\, =\, }\frac{\mathrm{2}P^{\mathrm{2}\, }\rho l}{\mathrm{3}WV_{m}^{\mathrm{2}}\,\mathrm{cos^{2}\phi }\, }}}$$
Now, the volume (say K1) of conductor material required in the 3-phase 4-wire overhead AC transmission system is given by,
$$\mathrm{\mathit{ K_{\mathrm{1}}\mathrm{\, =\, }\mathrm{3}a_{\mathrm{2}}l\mathrm{\, +\, }a_{n}l\mathrm{\, =\, }\mathrm{3.5}a_{\mathrm{2}}l}}$$
$$\mathrm{\mathit{\Rightarrow K_{\mathrm{1}}\mathrm{\, =\, }\mathrm{3.5}\times \left ( \frac{\mathrm{2}P^{\mathrm{2}\, }\rho l}{\mathrm{3}WV_{m}^{\mathrm{2}}\,\mathrm{cos^{2}\phi }\, } \right )\times l}}$$
$$\mathrm{\mathit{\therefore K_{\mathrm{1}}\mathrm{\, =\, }\frac{\mathrm{7}P^{\mathrm{2}\, }\rho l^{\mathrm{2}}}{\mathrm{3}WV_{m}^{\mathrm{2}}\,\mathrm{cos^{2}\phi }\, } }\: \: \: \cdot \cdot \cdot \left ( 2 \right )}$$
Now, comparing equations (1) & (2), we have,
$$\mathrm{\mathit{ \frac{K_{\mathrm{1}}}{K}\mathrm{\, =\, }\frac{\left ( \frac{\mathrm{7}P^{\mathrm{2}\, }\rho l^{\mathrm{2}}}{\mathrm{3}WV_{m}^{\mathrm{2}}\,\mathrm{cos^{2}\phi }\, } \right )}{\left ( \frac{\mathrm{2}P^{\mathrm{2}\, }\rho l^{\mathrm{2}}}{WV_{m}^{\mathrm{2}}\,\mathrm{cos^{2}\phi }\, } \right )}}\mathrm{\, =\, }\frac{7}{6}}$$
$$\mathrm{\mathit{\therefore K_{\mathrm{1}}}\mathrm{\, =\, }\frac{7}{6}\times \mathit{K}\: \: \: \cdot \cdot \cdot \left ( 3 \right )}$$
Hence, from eq. (3), it is clear that the volume of conductor material required in 3-phase 4-wire system is (7/6)th times of that required in 3-phase 3-wire overhead AC transmission system.
841 Views
To Continue Learning Please Login