Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
What is the Representation of DFA in compiler design?
Deterministic means that on each input there is one and only one state to which the automata can have the transition from its current state. In deterministic finite automata, the head can move only in one direction to scan the input tape symbols. But in the case of two-way, finite automata on scanning an input symbol the head of the tape may move in right or left from its current position.
A deterministic finite automata is a set of 5 tuples and defined as
M = (Q, Σ, δ, q0, F)
- Q: A non-empty finite set of states present in the finite control (q0, q1, q2).
- Σ: A Non-empty finite set of input symbols.
- δ: It is a transition function that takes two arguments, a state, and an input symbol, it returns a single state represented by ∴ δ: Q x Σ → Q. Let q is the state and a be the input symbol passed to the transition function. δ(q, a) = q. q is the output of the function, which may be the same or new state.
- $q_{0} \, \epsilon \, Q$ is the initial state.
- $F \subseteq Q$ is the set of final states.
There are two ways to represent Deterministic finite Automata −
Transition Diagram
It is a directed graph or flow chart having states and edges. The transition graphs were created by John Myhill in 1957. A strong path through a transition graph is a sequence of edges forming a path starting at some start state and ending at a final state. It can concentrate the string of letters so that label each edge in the path. It can make a word that is accepted by this machine. Thus, it can describe the transition graph as a collection of the following −
- A finite set of states, one of them named as the start state and some of which are named as the final state. The starting state is described by a circle having an arrow and the final state is described by two concentric circles. The diagrammatic representation is as follows −
Example
0, 1, 2→ States
0 → Initial State
2 → Final State
a, b → Input Symbols
An alphabet Σ of possible input letters from which input strings are formed.
A finite set of transitions (labelled edge) that shows how to go from one state to another state, based on reading defined substrings of input letters.
- Transition Table
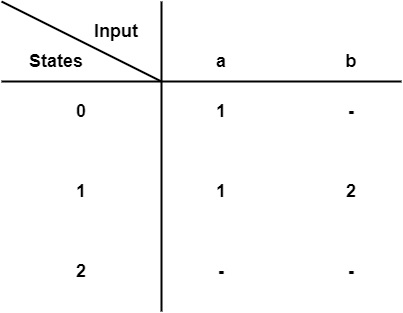
Finite Automata can be represented by 5 tuples (Q, Σ, δ, q0, F)
- Q is a finite non-empty set of states.
- Σ is a finite set of input symbols.
- $\delta$ is the transition function.
- q0 ∈ Q is the initial state.
- F ⊆ Q is the set of final states.
Example − Design Finite Automata which accepts string "abb".
Solution
States − Q = {q0, q1, q2, q3}
Input Symbols − Σ = {a, b}
Transition Function $\delta$− {$\delta$(q0, a) = q1,$\delta$ (q1, b) = q2, $\delta$(q2, b) = q3}
Initial State − q0
Final State (F) − {q3}
2K+ Views
