Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
What is minimizing of DFA in compiler design?
Minimizing means reducing the number of states in DFA. We have to detect those states of DFA whose presence or absence in DFA does not affect language accepted by DFA. These states can be eliminated from DFA.
Algorithm: Minimization of DFA
Input − DFA D1 with a set of states Q with a set of final states F.
Output − DFA D2 which accepts the same language as D1 and having a minimum number of states as possible.
Method
Make a partition 'π' of a set of states with two subsets −
- Final state 'F'
- Non-Final States 'Q-F'
∴ π={F,Q−F}
To apply the following procedure to make πnew from π.
For each set S of π
Partition S into subsets such that two states p & q of S are in the same subset of S if for each input symbol 'a' states p & q have transitioned to states in the same set of π. It can replace S in πnew with a set of subsets formed.
If πnew=π,let πfinal=π & continue with step 4. Else repeat step 2 for π =πnew.
Choose one state from each set of πfinal as representative of that set.
These states will be states of Minimized DFA D2.
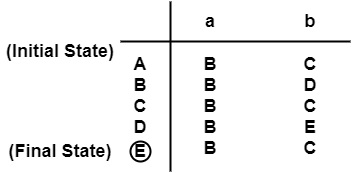
Example1 − Convert following DFA to Minimized DFA.
Solution
Make a transition table
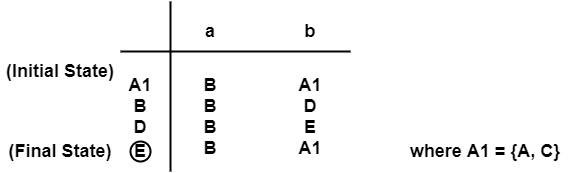
Make a partition ′π′ of set of states i.e., π ={F,Q−F}
∴ π0={{E},{A,B,C,D}}
For input symbol a, on {A, B, C, D} of π0
All B’s lie in the same set {A, B, C, D} of π0
For input symbol b, on {A, B, C, D} of π0
∴ {A,B,C,D}of π0 will be split into {A,B,C}and {D}
π1={{E},{A,B,C},{D}}
For input a, on {A, B, C} of π1
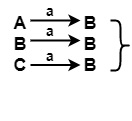
All B’s lie in the same set of π1
For input b on {A, B, C} of π1
∴ {A,B,C}in π1 will be split into {A, C} and {B}
∴ π2={{E},{A,C},{B},{D}}
Check if {A, C} can be splitted further (a)
- For input a, on {A, C} of π2
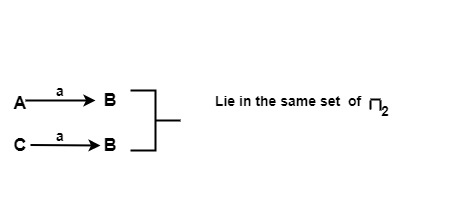
For input b, on {A, C} of π2
∴ {A,C} will not be splitted
∴ π3={{E},{A,C},{B},{D}}
∴ π3=π2=πfinal={{E},{A,C},{B},{D}}
∴ There will be 4 states of Minimized DFA corresponding to 5 states of given DFA.
{A, C} can be renamed as A1
B D E
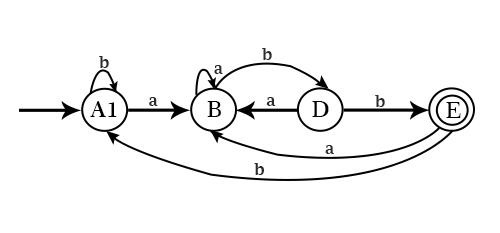
states of Minimized DFA, i.e., A1, B, D, E will be joined by seeing the transitions from the given DFA table.
Minimized or Reduced Automata will be
3K+ Views
