Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
What is Scott-T Transformer Connection?
The Scott-T connection is a method of connecting two 1-phase transformers to perform the 3- phase to 2-phase conversion and vice-versa. In the Scott connection, the two 1-phase transformers are connected electrically (not magnetically), where one transformer is known as main transformer and the other is called as auxiliary or teaser transformer.
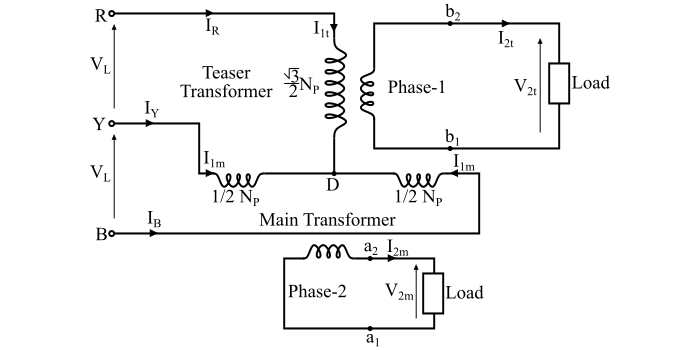
The connection diagram of the Scott connection is shown in the figure. The main transformer is the centre tapped transformer at point D and is connected across the lines Y and B of the 3- phase side. Thus, the primary of the main transformer is YB and the secondary is a1a2. The teaser transformer is connected between the line terminal R and the centre tapping point D. Thus, the teaser transformer has primary winding RD and the secondary winding b1b2.
Phasor Diagram of Scott-T Connection
The phasor diagram of the Scott connection is shown in the figure.
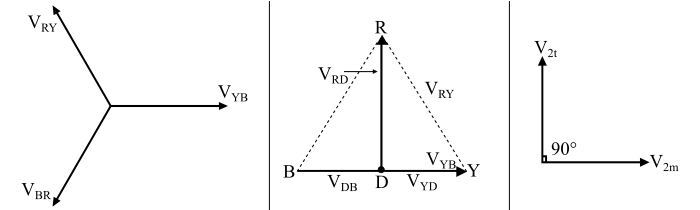
Here, the line voltages of the three-phase balanced supply system are −
$$\mathrm{𝑉_{𝑅𝑌} = 𝑉_{𝑌𝐵} = 𝑉_{𝐵𝑅} = 𝑉_{𝐿}}$$
Let VYB be taken as the reference phasor, then
$$\mathrm{𝑉_{𝑌𝐵} = 𝑉_{𝐿}\angle 0°}$$
$$\mathrm{𝑉_{𝑅𝑌} = 𝑉_{𝐿}\angle + 120°}$$
$$\mathrm{𝑉_{𝐵𝑅} = 𝑉_{𝐿}\angle − 120°}$$
The figure also shows the voltages on the primary windings of the main and teaser transformers. Since, the centre tapping point D divides the primary winding YB of the main transformer into two equal halves. Therefore,
$$\mathrm{Number\:of\:turns\:in\:portion\:𝑌𝐷 = Number\:of\:turns\:in\:portion\:𝐷𝐵 =\frac{𝑁_{𝑃}}{2}}$$
Hence, the voltages VYD and VDB are equal and in phase with the voltage VYB i.e.
$$\mathrm{𝑉_{𝑌𝐷} = 𝑉_{𝐷𝐵} =\frac{𝑉𝐵𝐶}{2}=\frac{𝑉_{𝐿}}{2}\angle 0° \:\:… (1)}$$
Now, the voltage between terminals R and D is
$$\mathrm{𝑉_{𝑅𝐷} = 𝑉_{𝑅𝑌} + 𝑉_{𝑌𝐷} = 𝑉_{𝐿}\angle 120° +\frac{𝑉_{𝐿}}{2}\angle 0°}$$
$$\mathrm{\Rightarrow\:𝑉_{𝑅𝐷} =[𝑉_{𝐿}(-\frac{1}{2}+𝑗\frac{√3}{2})]\:+\:[\frac{𝑉_{𝐿}}{2}(1\:+\:𝑗0)]}$$
$$\mathrm{\Rightarrow\: 𝑉_{𝑅𝐷} =𝑗\frac{√3}{2}𝑉_{𝐿}= 0.866\:𝑉_{𝐿}\angle 90° … (2)}$$
Thus, the primary voltage VRD of the teaser transformer is 0.866 times of that of the main transformer and is 90° displaced from it in time.
The voltage VRD is applied to the primary winding of the teaser transformer. Thus, the secondary terminal voltage V2t of the teaser transformer will lead the secondary terminal voltage V2m of the main transformer. For the same flux in each transformer, the voltage per turn should be the same. To make the voltage per turn same in the primary windings of the main and teaser transformers, the number of turns in the primary of the teaser transformer should be
$$\mathrm{Number\:of\:turns\:in\:winding\:𝑅𝐷,\:𝑁_{𝑅𝐷 }=\frac{√3}{2}𝑁_{𝑃}}$$
Then,
$$\mathrm{\frac{𝑉_{2𝑡}}{𝑁_{𝑆}}=\frac{𝑉_{𝑅𝐷}}{𝑁_{𝑅𝐷}}}$$
$$\mathrm{\Rightarrow\:𝑉_{2𝑡} =\frac{𝑁_{𝑆}}{𝑁_{𝑅𝐷}}𝑉_{𝑅𝐷} =(\frac{𝑁_{𝑆}}{\frac{√3}{2}𝑁_{𝑃}})(\frac{√3}{2}𝑉_{𝐿})}$$
$$\mathrm{\Rightarrow\:𝑉_{2𝑡} =\frac{𝑁_{𝑆}}{𝑁_{𝑃}}𝑉_{𝐿} = 𝑉_{2𝑚} … (3)}$$
Therefore, the secondary windings of both the main and teaser transformers have equal voltage in magnitude, but they are displaced by 90° in time so that they results in a balanced two-phase system.
Relationship between Input and Output Currents
Let, IR, IY and IB are the line currents on the 3-phase input side.
$$\mathrm{𝐼_{1𝑚} = Primary\:current\:of\:main \:transformer}$$
$$\mathrm{𝐼_{2𝑚} = Secondary\:current\:of\:main \:transformer}$$
$$\mathrm{𝐼_{1𝑡} = Primary\:current\:of\:teaser \:transformer}$$
$$\mathrm{𝐼_{2𝑡} = Secondary\:current\:of\:teaser \:transformer}$$
Now, from the connection diagram,
$$\mathrm{𝐼_{1𝑡} = 𝐼_{𝑅}}$$
As, the secondary windings of both the transformers are identical, thus,
$$\mathrm{|𝐼_{2𝑚}| = |𝐼_{2𝑡}| = 𝐼_{2}\:(say)}$$
If the magnetising current of the transformers is neglected, then the mmf balance equation of the teaser transformer is given by,
$$\mathrm{𝐼_{1𝑡}𝑁_{𝑅𝐷} = 𝐼_{2𝑡}𝑁_{𝑆}}$$
$$\mathrm{\Rightarrow\:𝐼_{𝑅}(\frac{√3}{2}𝑁_{p})}=𝐼_{2𝑡}𝑁_{𝑆}$$
Therefore,
$$\mathrm{𝐼_{𝑅} = 𝐼_{1𝑡} =\frac{2}{√3}(\frac{𝑁_{𝑆}}{𝑁_{𝑃}})𝐼_{2𝑡} = 1.15\:𝐾\:𝐼_{2𝑡}\:\: … (4)}$$
Where, 𝐾 =$(\frac{𝑁_{𝑆}}{𝑁_{𝑃}})$ is the transformation ratio of the transformer. Hence,
$$\mathrm{𝐼_{2𝑡} =\frac{2}{√3}(\frac{𝐼_{𝑅}}{𝐾})}\:… (5)$$
Now, the MMF balance equation of the main transformer is,
$$\mathrm{𝐼_{1𝑚}𝑁_{𝑌𝐷} − 𝐼_{1𝑚}𝑁_{𝐵𝐷} = 𝐼_{2𝑚}𝑁_{𝑆}}$$
$$\mathrm{\Rightarrow\:𝐼_{𝑌}(\frac{𝑁_{𝑃}}{2})− 𝐼_{𝐵}(\frac{𝑁_{𝑃}}{2})= 𝐼_{2𝑚}𝑁_{𝑆}}$$
$$\mathrm{\Rightarrow\: 𝐼_{𝑌} − 𝐼_{𝐵} = 2(\frac{𝑁_{𝑆}}{𝑁_{𝑃}})𝐼_{2𝑚} = 2\:𝐾\:𝐼_{2𝑚}\:… (6)}$$
Therefore,
$$\mathrm{𝐼_{2𝑚} =\frac{1}{2}({\frac{𝐼_{𝑌} − 𝐼_{𝐵}}{𝐾}})\:\:… (7)}$$
Now, for a balanced 3-phase system,
$$\mathrm{𝐼_{𝑅} + 𝐼_{𝑌} + 𝐼_{𝐵} = 0}$$
$$\mathrm{∴\: 𝐼_{𝐵} = −𝐼_{𝑅} − 𝐼_{𝑌}\: … (8)}$$
Substituting the value of IB in the equation (6), we get,
$$\mathrm{𝐼_{𝑌} − (−𝐼_{𝑅} − 𝐼_{𝑌}) = 2\:𝐾\:𝐼_{2𝑚}}$$
$$\mathrm{\Rightarrow\: 2𝐼_{𝑌} + 𝐼_{𝑅} = 2\:𝐾 \:𝐼_{2𝑚}}$$
$$\mathrm{\Rightarrow\:𝐼_{𝑌} = −\frac{𝐼_{𝑅}}{2}+ 𝐾\: 𝐼_{2𝑚} … (9)}$$
Again, substituting the value of current IY in eq. (8), we have,
$$\mathrm{𝐼_{𝐵} = −𝐼_{𝑅} −(-\frac{𝐼_{𝑅}}{2})+ 𝐾 \:𝐼_{2𝑚})}$$
$$\mathrm{\Rightarrow\:𝐼_{𝐵} = −\frac{𝐼_{𝑅}}{2}− 𝐾 \:𝐼_{2𝑚} … (10)}$$
These current equations are valid for balanced as well as unbalanced loads.
Applications of Scott-T Connection
The Scott connection of transformer is used in following applications −
The Scott connection is used to link a 3-phase system with a 2-phase system with the flow of power in either direction.
It is used to operate two 1-phase electric furnaces together when the power is drawn from the 3-phase supply.
It is also used to supply 1-phase loads such as electric trains from the balanced three phase supply.
6K+ Views
