Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
What is Polar Curve in Illumination?
Polar Curves
The plots drawn between the candle power and angular position are known as polar curves. Due to unsymmetrical shape of the lamps, the luminous intensity is not uniform in all directions. The luminous intensity in all directions can be represented with the help of polar curves.
The polar curves are drawn by taking the luminous intensities in various directions at an equal angular displacement in the sphere. A radial ordinate pointing in any particular direction on a polar curve represents the luminous intensity of the source when it is viewed from the direction.
Therefore, the polar curves are classified into two types viz. −
Horizontal Polar Curve
Vertical Polar Curve
Horizontal Polar Curve
When a curve is plotted between the candle power and the angular position, and the candle power is measured in the horizontal plane about the vertical axis, then the polar curve is called the horizontal polar curve.
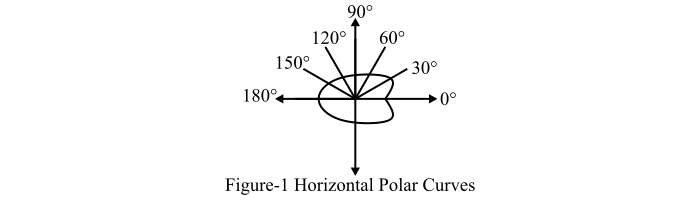
Figure-1 shows the typical horizontal polar curve for an ordinary lamp. In this curve, the dip at 90° is due to coiled coil filament.
Vertical Polar Curve
When a curve is plotted between the candle power and the angular position, and the candle power is measured in the vertical plane about the horizontal axis, then the polar curve is called the vertical polar curve.
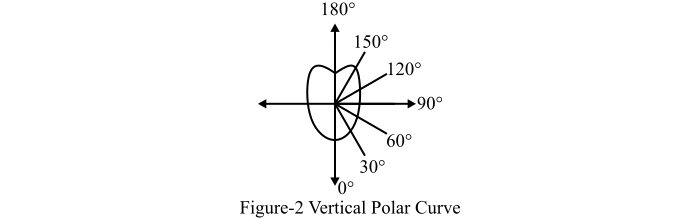
A typical vertical polar curve for an ordinary lamp is shown in Figure-2. The depression at 180° in the vertical polar curve is due to the position of the lamp holder.
Polar curves are used to determine the following
The actual illumination of a surface.
Mean horizontal candle power (MHCP).
Mean spherical candle power (MSCP).
Note – The mean spherical candle power (MSCP) of a symmetrical source of light can be determined using the polar curves by means of Rousseau's Construction.
Rousseau's Construction
Consider a vertical polar curve in the form of two lobes that are symmetrical about the vertical axis YOY'. A simple Rousseau's curve is shown in Figure-3.
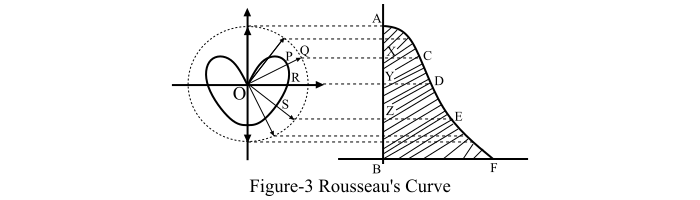
The steps followed for the construction of the Rousseau's curve are −
Step (1) – Draw a circle with any convenient radius with 'O' as center.
Step (2) – Draw a line 'AB' parallel to the axis YOY' and is equal to the diameter of the circle.
Step (3) – Draw any line OPQ meeting the polar curve at P and the circle at Q. Now, let the projection be 'X' onto the parallel line 'AB'.
Step (4) – At 'X', erect an ordinate as XC = OP.
Step (5) – Now from the line 'AB' ordinate equals the corresponding radius on the polar curve are set up such as YD = OR, ZE = OS and so on.
Step (6) – The curve ACDEFBA so obtained by joining these ordinates is known as Rousseau's curve.
The mean ordinate of the Rousseau's curve gives the mean spherical candle power (MSCP) of the lamp having polar curve given in Figure-3.
Therefore, the mean ordinate of the curve is,
$$\mathrm{Mean\: ordinate\: =\: \frac{Area\: of\: \mathit{ACDEFBA}}{Length\: of\: \mathit{AB}}}$$
Where, the area under curve can be determined by using a graph or by Simpson's rule.
6K+ Views
To Continue Learning Please Login