Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
What is Lambert's Cosine Law? (Laws of Illumination)
The light received by any surface depends upon the angle made by the normal to the surface, to the light flux. The Lambert's cosine law of illumination explains the relation between the illumination of the surface and the cosine of the angle.
Statement
The Lambert's cosine law of illumination states that
"The illumination of a surface is directly proportional to the cosine of the angle between the normal to the surface and the direction of incident light".
That is,
$$\mathrm{\mathit{E}\propto cos\, \theta \: \: \: \cdot \cdot \cdot \left ( 1 \right )}$$
Explanation
Case I – Consider a surface that is normal to the luminous flux as shown in Figure-1.
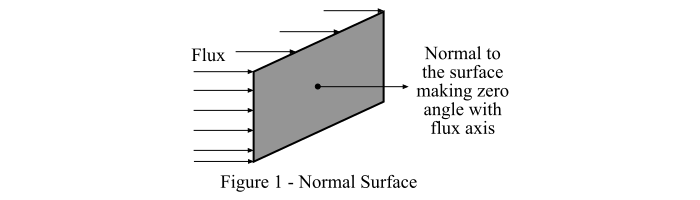
Then, as per Lambert's cosine law, we get,
$$\mathrm{Illumination,\mathit{E}=\frac{\phi }{\mathit{A}}\: \: \: \cdot \cdot \cdot \left ( 2 \right )}$$
Case II – Consider a surface inclined to the flux in such a way that the normal to the surface makes an angle (θ) to the flux axis, as shown in Figure-2.
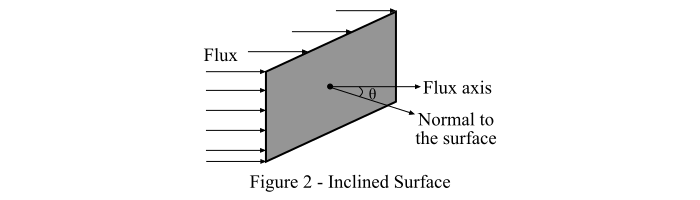
Then, by the Lambert's cosine law, we get,
$$\mathrm{\mathit{E}=\frac{\phi }{\mathit{A}}\times cos\, \theta \: \: \: \cdot \cdot \cdot \left ( 3 \right )}$$
Case III – Consider a point 'P' on a plane surface and the distance between the source of light (S) and the point 'P' is 'r' meters. The source (S) is located at height of 'h' meters from the surface and its luminous intensity is 'I' candle power as shown in Figure-3.
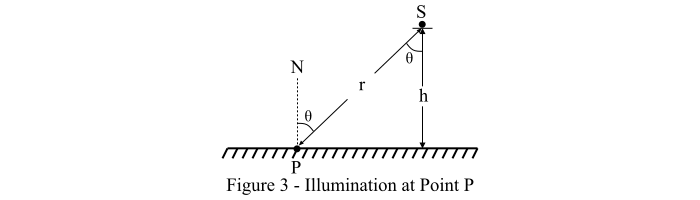
Then, by the cosine law of illumination, we get, the illumination at point 'P' as,
$$\mathrm{\mathit{E_{P}}=\mathit{\frac{I }{r^{\mathrm{2}}}}\times cos\, \theta}$$
From Figure-3, we have,
$$\mathrm{cos\, \theta \: =\: \mathit{\frac{h}{r}}}$$
$$\mathrm{\Rightarrow \mathit{r} \: =\: \frac{\mathit{h}}{cos\, \theta}}$$
Therefore, the illumination at point 'P' is,
$$\mathrm{\mathit{E_{P}}\: =\: \mathit{\frac{I }{\left ( \mathit{h}/\mathrm{cos\, \theta }\right )^{\mathrm{2}}}}\times cos\, \theta}$$
$$\mathrm{\therefore \mathit{E_{P}}\: =\: \mathit{\frac{I }{\mathit{h}^{\mathrm{2}}}}\times cos^{3}\, \theta\: \: \: \cdot \cdot \cdot \left ( 4 \right )}$$
Where, I/h2 is the illumination at any point located directly below the source of light.
9K+ Views
