Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
What is a ROC Curve and its usage in Performance Modelling?
Introduction
Machine learning models are essential for successful AI implementation since they represent the mathematical underpinnings of artificial intelligence. The quality of our AI depends entirely on the machine models that power it. We require a method for objectively evaluating our machine learning model's performance and deciding whether it is suitable for use. If we had a ROC curve, that would be useful.
Everything that we need to learn about ROC curves is covered in this article.
ROC Curve
A Receiver Operating Characteristic (ROC) curve is a graphical representation of the performance of a binary classification model. It plots the true positive rate (TPR) against the false positive rate (FPR) at various threshold settings. The ROC curve is a useful tool for evaluating the performance of a classifier, as it allows for the visualization of the tradeoff between the sensitivity and specificity of the model.
In a binary classification problem, a model attempts to predict the class of an observation based on a set of input features. The two possible classes are typically labeled as "positive" and "negative". A true positive (TP) is an instance where the model correctly predicts the positive class, while a false positive (FP) is an instance where the model incorrectly predicts the positive class. Similarly, a true negative (TN) is an instance where the model correctly predicts the negative class. In contrast, a false negative (FN) is an instance where the model incorrectly predicts the negative class.
The TPR, also known as sensitivity or recall, is the proportion of true positives among all positive instances. It is calculated as TP / (TP + FN). The FPR, also known as the fall-out, is the proportion of false positives among all negative instances. It is calculated as FP / (FP + TN).
Plotting the TPR versus the FPR for a model at various threshold settings results in a ROC curve. The probability threshold for classifying an instance as positive is determined by the threshold setting. Assume, for instance, that the threshold is set at 0.5. In that situation, instances with expected probabilities more than 0.5 will be classed as positive instances, whilst instances with predicted probabilities lower than 0.5 would be classified as negative instances. We can observe how the trade-off between TPR and FPR varies when the threshold changes by adjusting the threshold.
The ROC curve is a useful tool for assessing the effectiveness of a classifier since it makes it possible to see how the trade-off between the model's sensitivity and specificity is represented. AUC, or the area under the ROC curve, is a regularly used metric to assess a classifier's general performance .An AUC of 1 would represent a perfect classifier, while an AUC of 0.5 would represent a classifier that was chosen at random. If a model's AUC is close to 1, it is regarded as an excellent classifier; if it is close to 0.5, it is regarded as a poor classifier.
Together with classifier performance analysis, ROC curves can be used for model selection. The classifier with the highest AUC when comparing different classifiers is typically thought to be the best.
Model Performance Hypothesis
A ROC curve plots the true positive rate (TPR) against the false positive rate (FPR) at various threshold settings. A model with a high TPR and low FPR will have a ROC curve that hugs the top left corner of the plot, indicating good performance.
The AUC measures the overall performance of a model and ranges from 0 to 1. A model that operates perfectly and accurately categorizes every case has an AUC of 1. A model with an AUC of 0.5 is equivalent to guessing at random. AUC values between 0.5 and 1 show that the model outperforms conjecture. A higher AUC value often indicates a better performing model.
In addition to the ROC curve and AUC, other assessment measures, such as precision, recall, F1 score, and accuracy, can be used to determine how well the model performs.
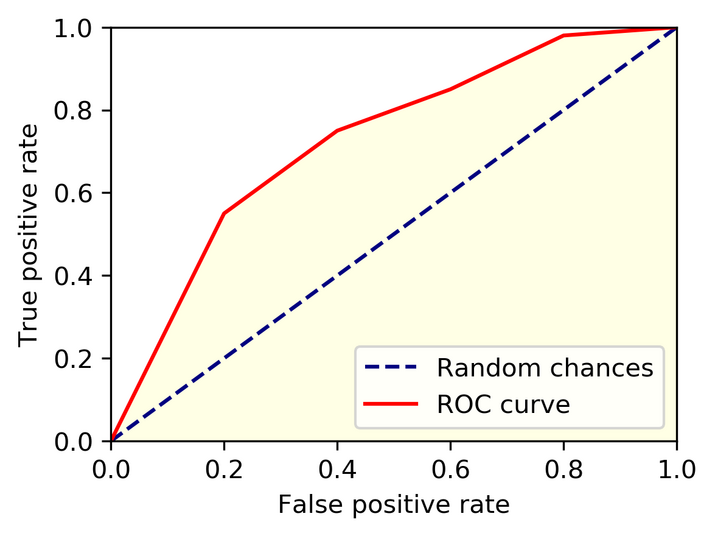
The problem's context and the requirements of the application should also be considered. For instance, in some circumstances, precision may be more crucial than excellent recall (sensitivity), while the converse may be true. Model performance evaluation should also be carried out on a different test dataset to avoid overfitting and provide a more precise performance estimate.
ROC Curve for the Multi-Class Model
A Receiver Operating Characteristic (ROC) curve is a graphical representation of the performance of a binary classifier. The curve plots the true positive rate (TPR) against the false positive rate (FPR) at various threshold settings. One way to expand the ROC curve analysis in a multi-class model is to use one-vs.-all comparisons. Whereas every other class is viewed as the negative case, every class is viewed as the positive case. As a result, there are as many ROC curves as classes, and each curve shows how well the classifier performed for a particular class. The ROC of all the classes can also be combined using micro- and macro-averages.
Conclusion
In conclusion, the ROC curve is a useful tool for evaluating the efficacy of a binary classifier. One-vs-all comparisons or the combination of the ROC of all the classes using micro- and macro-averages might prolong the ROC curve when working with a multi-class model. A powerful classifier will create a ROC curve that is in the top-left corner of the plot thanks to a high True Positive Rate (TPR) and a low False Positive Rate (FPR). The area under the ROC curve (AUC), which is frequently used as a statistic to evaluate a classifier's performance, shows greater performance when it is larger.
298 Views
