What is a Sinusoidal Wave Signal – Definition and Importance

A sinusoidal wave signal is a type of periodic signal that oscillates (moves up and down), periodically. The geometrical waveform of a sinusoidal signal forms an S-shape wave in one complete cycle. A sinusoidal can be a sine functioned signal or cosine functioned signal. Thus, a sinusoidal signal can be defined as,

$$\mathrm{y=sin\, x}$$

$$\mathrm{y=cos\, x}$$

Both sine and cosine signals are the types of sinusoidal wave signals. But, the cosine signal is advanced with respect to the sine signal by 90° in time. The sinusoidal wave signal has a smooth wave that oscillates above and below zero and used in technical analysis of systems.

In this article, we will discuss learn the definition and important of the sinusoidal wave signal in context of electrical and electronics circuits. But, first it is important to understand that what a signal is.

What is a Signal?

An electrical quantity like voltage or current which is used for carrying information from one point to another through a medium such as cable, electromagnetic radiation, etc. is known as a signal. In practice, a single consists of two major parts namely message signal and carrier signal. The message signal represents the information to be shared, while the carrier signal represents the energy that is required for the flow of signal from one point to another.

We generally plot a graph between values of a single at different time instants to analyze the behavior of the signal. This graph is known as the graphical representation of the signal. However, in most cases, we express a signal by using mathematic equations.

What is a Sinusoidal Wave Signal?

A smooth periodic signal that is expressed in terms of sine or cosine trigonometric functions is called as a sinusoidal signal. It is also known as sinusoid. A sinusoidal wave signal has a waveform of S-shape over a single time period. A sinusoidal wave signal is generally depicted as two semi-circular curves that alternate above and below the time axis.

The following function represents a sinusoidal wave signal −

$$\mathrm{x\left ( t \right )=sin\, \omega t}$$

Or,

$$\mathrm{x\left ( t \right )=cos\, \omega t}$$

A sinusoidal wave signal can be of two types namely sine wave signal and cosine wave signal. The sine wave signal starts from zero and covers positive values of magnitude and again reaches to zero along the time axis, this travel of the signal is called positive half cycle of the signal. Again, the signal starts from zero and convers the negative values of the magnitude and reaches to the zero, this travel is referred to as the negative half cycle of the signal. The total duration of positive and negative half cycles together is known as the single cycle of the sine wave signal.

On the other hand, the cosine wave signal also completes one cycle through the positive half cycle and negative half cycle. But, the cosine single is 90° advanced in time with respect to the sine wave signal.

A sinusoidal wave signal has different values of the quantity at different instants of time. The value of the sinusoidal wave signal at a particular point of time is called the instantaneous value of the signal. Thus, a sinusoidal wave signal is a function of time and therefore is written as x(t). The maximum value of the sinusoidal wave signal is called amplitude. A typical sine wave signal is shown in the following figure.

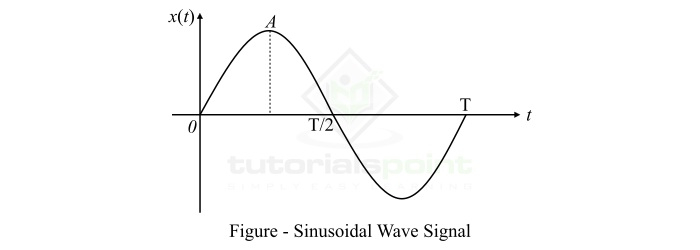
Here, A is the amplitude of the signal, ω is the angular frequency of the signal. The frequency is defined as the number of cycles completed by the signal in unit time. Frequency is measured in Hertz, denoted by Hz. Thus, for the given sinusoidal signal, the frequency is given by,

$$\mathrm{f=\frac{1}{T}}$$

Where, T is the time period of the signal, and is defined as the time required to complete one cycle. The higher value of frequency indicates that a sinusoidal signal completes more oscillations or cycles in less amount of time.

It is not necessary for a sinusoidal signal to start from the zero time, instead it may also start after certain duration of time. This duration of time after which the sinusoidal wave signal starts with respect to the point of zero time is indicated in terms of phase difference, denoted by the symbol phi (Ï•). It is measured in degrees or radians.

From the above figure, it is also clear that a sinusoidal signal is a periodic signal because it keeps repeating its pattern after one wavelength.

The electrical energy that we receive in our home, office, and industries is produced and utilized in the form of sinusoidal signals. The standard frequency of these sinusoidal signals is 50 Hz in India and British countries, and 60 Hz in American countries.

Importance of Sinusoidal Wave Signals

Sinusoidal wave signals are very important in electrical and electronics engineering, and all other sub-branches of electrical engineering. The sinusoidal signals are so important because the mathematical operations like sum, subtraction, multiplication, differentiation, integration, etc. of a sinusoidal signal also produce a sinusoidal signal.

Another important point is that according to Fourier Series Theory, a complex sinusoidal signal can be written in terms of simple sine and cosine signals. Thus, its mathematical analysis is easy which is extensive used for analyzing different electrical systems.

Note − A sine wave sinusoidal signal is most commonly used in power systems worldwide as it starts from zero value. Thus, all the electrical appliances are designed to work satisfactorily on sine wave sinusoidal signal.

Sinusoidal Signal Parameters

Listed below are all the important parameters of a sinusoidal signal −

• Amplitude − It is the maximum value of the sinusoidal signal. It is also called peak value or maximum value.

• Instantaneous Value − It is the value of the sinusoidal signal at a particular time instant. It is different at different time instants.

• Peak to Peak Value − The value of the sinusoidal signal measured between the positive peak and negative peak is referred to as peak to peak value. It is double of the maximum value.

• Average Value − It is the average of different instantaneous values of the sinusoidal signal over a complete cycle. For sinusoidal signal, the average value over one complete cycle is zero.

• RMS Value − RMS stands for Root Mean Square. It is the value of sinusoidal signal that represents the equivalent amount of DC power.

• Time Period − It is the length of one complete cycle of the sinusoidal signal measured on the time axis.

• Frequency − It is the number of cycle per second that the sinusoidal signal completes. It shows how fast the signal is changing in time.

• Time Delay − Time delay represents the lag or lead of one sinusoidal signal with respect to another sinusoidal signal in time domain.

Conclusion

In this article, we discussed in detail the importance of sinusoidal signals in the field of electrical and electronics engineering, and all the important parameters of sinusoidal signals.