Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Weight-Biased Leftist Trees in Data Structure
Here we will see another variation of Leftist Tree. Here we will consider the number of nodes in a subtree, rather than the length of a shortest path for root to external node. Here we will define the weight w(x) of node x, to be the number of internal nodes in the subtree with root x. If x is an external node, then the weight is 0. If x is internal node, then the weight is one more than the sum of weights of its children.
Here is an example of Weight Biased Leftist Tree (WBLT) −
Suppose the Binary tree is like this −
If we calculate w(x) values for each node, it will be like this −
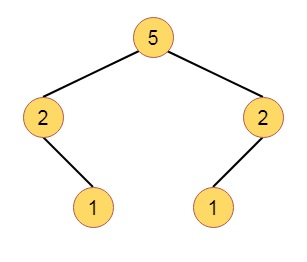
Now the definition of WBLT is like −
A binary tree is called Weight Balanced Leftist Tree if and only if, at every internal node the w(x) of left child is greater than or equal to the w(x) of the right child. A max (min) WBLT is a max (min) tree that is also a WBLT.
870 Views
