Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Range Trees in Data Structure
A range tree is defined as an ordered tree data structure to hold a list of points. It permits all points within a given range to be efficiently retrieved, and is typically implemented in two or higher dimensions. It is same to a kd-tree except with faster query times of O(logd n + k) but worse storage of O(n logd-1 n), with d indicating the dimension of the space, n indicating the number of points in the tree, and k indicating the number of points retrieved for a given query. Range trees may be differentiated with interval trees: instead of storing points and allowing points in a given range to be retrieved efficiently, an interval tree stores intervals and allows the intervals containing a given point to be retrieved efficiently.
Data Structure
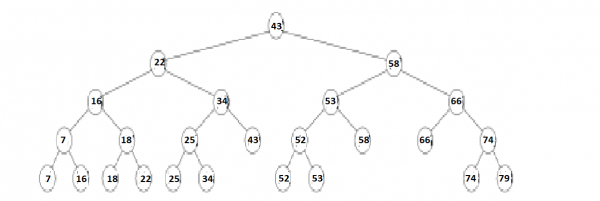
An example of a 1-dimensional range tree. Each node other than leaf stores the highest value in its left subtree.
A range tree on a set of 1-dimensional points is treated as a balanced binary search tree on those points. The points stored in the tree are stored in the leaves of the tree; each internal node stores the maximum value contained in its left subtree. A range tree on a set of points in d-dimensions is a recursively defined multi-level binary search tree. Each level of the data structure is treated as a binary search tree on one of the d-dimensions. The first level is a binary search tree on the first of the d-coordinates. Each vertex v of this tree consists of an associated structure that is a (d−1)-dimensional range tree on the last (d−1)-coordinates of the points stored in the subtree of v.
Operations
Construction
A 1-dimensional range tree on a set of n points is a binary search tree, which can be built in O(n log n) time. Range trees in higher dimensions are built recursively by constructing a balanced binary search tree on the first coordinate of the points, and after that, for each vertex v in this tree, building a (d−1)-dimensional range tree on the points contained in the subtree of v. Building a range tree this way would require O(n logdn) time.
3K+ Views
