Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Interval Trees in Data Structure
In this section we will see what is the interval tree. As the name suggests, that the interval trees are the trees which are associated with the intervals. So before discussing about the interval trees, let us see the elementary intervals.
An interval is basically a range. So if one interval is written as [a, b] it indicates that the range is starting from a, and ending at b.
Now suppose there is an interval [10, 20]. So there are three range values. First one is -∞ to 10, 10 to 20 and finally 20 to ∞
Now, suppose we will create second interval from [15, 25]. So this will be like −
Making another interval from [18, 22], So it will be like −
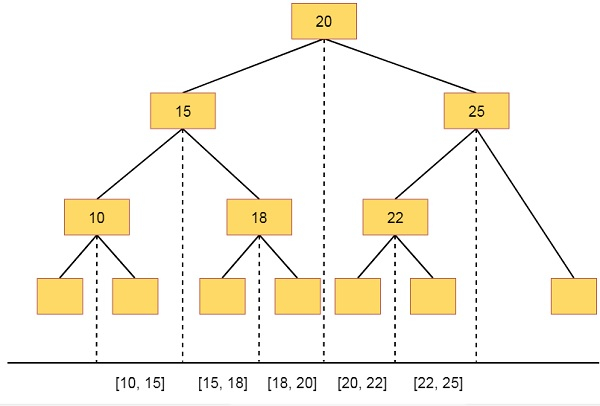
So there are different intervals and the sub-intervals. They are like below
| Interval Name | Interval Range | Sub-intervals |
| Interval 1 | [10, 20] | [10, 15], [15, 18], [18, 20] |
| Interval 2 | [15, 25] | [15, 18], [18, 20], [20, 22], [22, 25] |
| Interval 3 | [18, 22] | [18, 20], [20, 22] |
We can make an interval tree, from this information. The sub-intervals will be placed inside sub-trees.
In Interval tree, every leaf node is representing every elementary interval. On top of these leaves, is build a complete binary tree.
1K+ Views
