Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Huffman Trees in Data Structure
Definition
Huffman coding provides codes to characters such that the length of the code depends on the relative frequency or weight of the corresponding character. Huffman codes are of variable-length, and without any prefix (that means no code is a prefix of any other). Any prefix-free binary code can be displayed or visualized as a binary tree with the encoded characters stored at the leaves.
Huffman tree or Huffman coding tree defines as a full binary tree in which each leaf of the tree corresponds to a letter in the given alphabet.
The Huffman tree is treated as the binary tree associated with minimum external path weight that means, the one associated with the minimum sum of weighted path lengths for the given set of leaves. So the goal is to construct a tree with the minimum external path weight.
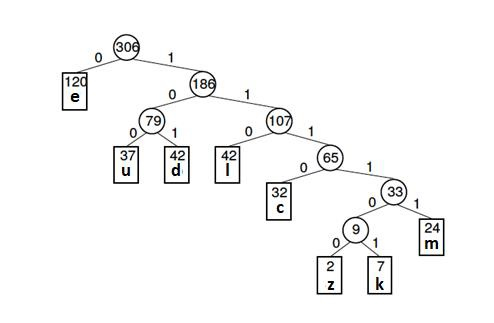
An example is given below-
Letter frequency table
| Letter | z | k | m | c | u | d | l | e |
| Frequency | 2 | 7 | 24 | 32 | 37 | 42 | 42 | 120 |
Huffman code
| Letter | Freq | Code | Bits |
|---|---|---|---|
| e | 120 | 0 | 1 |
| d | 42 | 101 | 3 |
| l | 42 | 110 | 3 |
| u | 37 | 100 | 3 |
| c | 32 | 1110 | 4 |
| m | 24 | 11111 | 5 |
| k | 7 | 111101 | 6 |
| z | 2 | 111100 | 6 |
The Huffman tree (for the above example) is given below -
10K+ Views
