- Trending Categories
Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Level Linked (2,4)-Trees in Data Structure
In this section we explain how (2,4)-trees can support efficient finger searches by the introduction of level links. The ideas explained in this section also implements to the more general class of height-balanced trees denoted (a, b)-trees, for b ≥ 2a.
A (2,4)-tree is defined as a height-balanced search tree where all leaves have the same depth and all internal nodes have degree two, three or four. Elements are stored at the leaves, and internal nodes only store search keys to guide searches. Since each internal node has degree at least two, it follows that a (2,4)-tree has height O(log n) and supports searches in O(log n) time. An important property of (2,4)-trees is that insertions and deletions provided by a finger take amortized O(1) time (this property is not shared by (2, 3)-trees, where there exist sequences of m insertions and deletions requiring Θ(m log m) time). Furthermore a (2,4)-tree with m leaves can be split into two trees of size m1 and m2 in amortized O(log min(m1, m2)) time. Similarly two (2,4)-trees of size m1 and m2 can be joined (concatenated) in amortized O(log min(m1, m2)) time.
For supporting finger searches, (2,4)-trees are augmented with level links, such that all nodes with equal depth are linked together in a double linked list. Following figure displays a (2,4)-tree augmented with level links. Remember all edges represent bidirected links. The additional level links are straightforward to preserve during insertions, deletions, splits and joins of (2,4)-trees.
To accomplish a finger search from X to Y we first check whether Y is to the left or right of X. Assume without loss of generality that Y is to the right of X. We then visit the path from X towards the root while examining the nodes V on the path and their right neighbours until it has been established that Y is contained within the subtree rooted at V or V’s right neighbour. The upwards search is then terminated and at most two downwards searches for y is started at respectively V and/or V’s right neighbour. In Figure 1 the pointers followed during a finger search from j to t are denoted by thick lines.
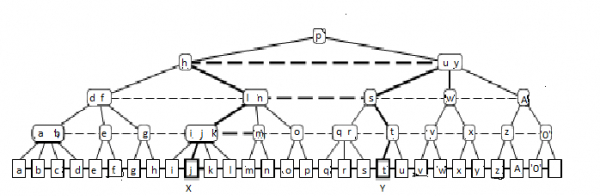
The O(log d) search time follows from the observation that if we advance the upwards search to the parent of node V then Y is to the right of the leftmost subtree of V′s right neighbour, i.e. d is at least exponential in the height reached so far.
In Figure 1 we advance from the internal node labelled “l n” to the node labelled “h” because from “s” we know that Y is to the right of the subtreeroorted at the node “q r”.
The construction for level linked (2,4)-trees generalizes directly to level linked (a, b)-trees that can be implemented in external memory. By selecting a = 2b and b such that an internal node fits in a block in external memory, we achieve external memory finger search trees supporting insertions and deletions in O(1) memory transfers, and finger searches with O(logb n) memory transfers.
435 Views
