Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Tournament Trees, Winner Trees and Loser Trees in Data Structure
Here we will see the Tournament trees, Winner and Looser trees. The Tournament tree is a complete binary tree with n external nodes and n – 1 internal nodes. The external nodes represent the players, and the internal nodes are representing the winner of the match between the two players. This tree is also known as Selection tree.
There are some properties of Tournament trees. These are like below −
This tree is rooted. So the link in the tree and directed path from parent to children, and there is a unique element with no parents
The parent value is less or equal to that node to general any comparison operators, can be used as long as the relative value of the parent and children are invariant throughout the tree
Trees with a number of nodes not a power of 2, contain holes. Holes can be present at any place in the tree.
This tree is a proper generalization of binary heaps
The root will represent overall winner of the tournament.
There are two types of Tournament Trees −
Winner Tree
Looser Tree
Winner Tree
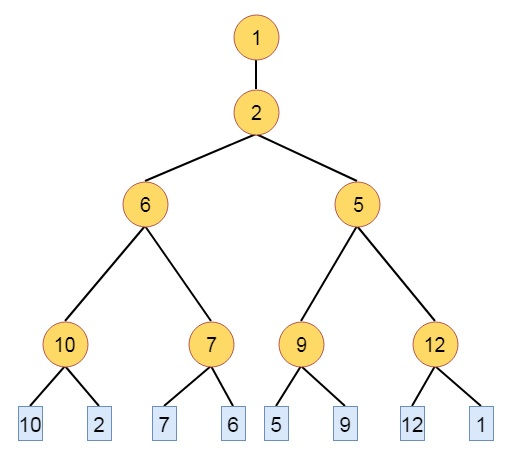
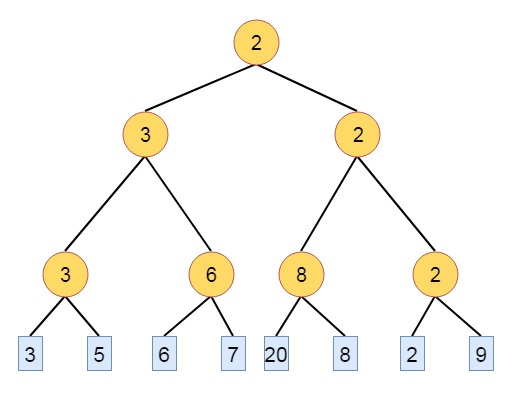
Winner tree is a complete binary tree, in which each node is representing the smaller or greater of its two children, is called winner tree. The root is holding the smallest or greatest node of the tree. The winner of the tournament tree is the smallest or greatest n key in all the sequences. It is easy to see that winner tree can be formed in O(log n) time.
Example − Suppose there are some keys, 3, 5, 6, 7, 20, 8, 2, 9
Looser Tree
Looser Trees are complete binary tree for n players where n external nodes and n – 1 internal nodes are present. The looser of the match is stored in the internal nodes. But in this overall winner is stored at tree[0]. The looser is an alternative representation, that stores the looser of a match at the corresponding node. An advantage of the looser is that, to restructure the tree after winner tree been output, it is sufficient to examine node on the path from leaf to root rather than the sibling of the nodes on this path.
Example − To form a looser tree, we have to create winner tree at first.
Suppose there are some keys, 10, 2, 7, 6, 5, 9, 12, 1. So we will create minimum winner tree at first.
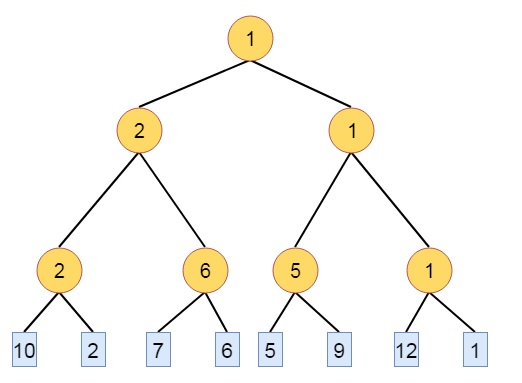
Now, we will store looser of the match in each internal node.
4K+ Views
