Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Sum of the mirror image nodes of a complete binary tree in an inorder way in C++
In this problem, we are given a complete binary tree. Our task is to create a program to find the sum of the mirror image nodes of a complete binary tree in an inorder way.
Here, we have to find the inorder traversal of the left sun-tree, and then for each node, we will add the mirror image with it. This means if we are traversing the left leaf node, we will add the value of the right leaf node with it. As it is the mirror image node.
Some important definitions
Complete binary tree is a binary tree where all levels have the highest number of nodes except the last level.
Inorder traversal is a tree traversal technique in which the left subtree is visited first, the root is visited and the right sub-tree is visited.
Let’s take an example to understand the problem,
Input
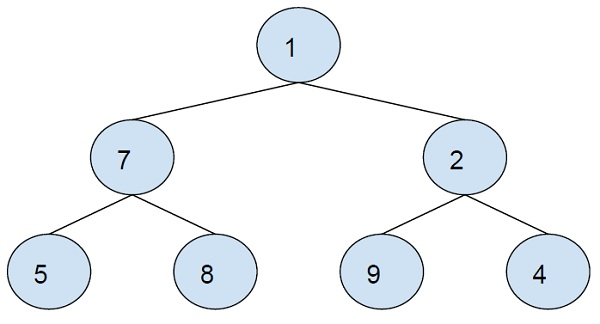
Output − 9 9 17 2
Explanation − Inorder traversal of the left subtree is 5-7-8-1.
Adding all nodes will mirror images.
5 + 4 = 9 7 + 2 = 9 8 + 9 = 17 1 + 1 = 2
To solve this problem, we will traverse the binary tree using inorder traversal. We will use two nodes, one to traverse the left subtree and the other to visit the mirror of the node. For example, we have a root node for the left subtree and for it we will have the mirrorroot that will traverse the mirror image of it.
Example
Program to illustrate the working of the solution,
#include <iostream>
using namespace std;
typedef struct node {
int data;
struct node* left;
struct node* right;
node(int d){
data = d;
left = NULL;
right = NULL;
}
} Node;
void printMirrorSum(Node* root, Node* rootMirror){
if (root->left == NULL && rootMirror->right == NULL)
return;
printMirrorSum(root->left, rootMirror->right);
cout<<(root->left->data + rootMirror->right->data)<<endl;
printMirrorSum(root->right, rootMirror->left);
}
int main(){
Node* root = new Node(1);
root->left = new Node(7);
root->right = new Node(2);
root->left->left = new Node(5);
root->left->right = new Node(8);
root->right->left = new Node(9);
root->right->right = new Node(4);
cout<<"Sum of node and mirror image nodes are :\n";
printMirrorSum(root, root);
if (root)
cout<<(root->data + root->data);
return 0;
}Output
Sum of node and mirror image nodes are : 9 9 17 2
75 Views
To Continue Learning Please Login