Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Inorder Traversal of a Threaded Binary Tree in C++
Here we will see the threaded binary tree data structure. We know that the binary tree nodes may have at most two children. But if they have only one children, or no children, the link part in the linked list representation remains null. Using threaded binary tree representation, we can reuse that empty links by making some threads.
If one node has some vacant left or right child area, that will be used as thread. There are two types of threaded binary tree. The single threaded tree or fully threaded binary tree.
For fully threaded binary tree, each node has five fields. Three fields like normal binary tree node, another two fields to store Boolean value to denote whether link of that side is actual link or thread.
| Left Thread Flag | Left Link | Data | Right Link | Right Thread Flag |
This is the fully threaded binary tree
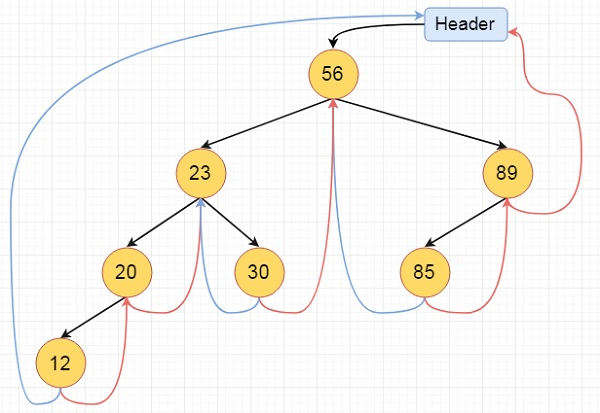
Algorithm
inorder(): Begin temp := root repeat infinitely, do p := temp temp = right of temp if right flag of p is false, then while left flag of temp is not null, do temp := left of temp done end if if temp and root are same, then break end if print key of temp done End
Example
#include <iostream>
#define MAX_VALUE 65536
using namespace std;
class N { //node declaration
public:
int k;
N *l, *r;
bool leftTh, rightTh;
};
class ThreadedBinaryTree {
private:
N *root;
public:
ThreadedBinaryTree() { //constructor to initialize the variables
root= new N();
root->r= root->l= root;
root->leftTh = true;
root->k = MAX_VALUE;
}
void insert(int key) {
N *p = root;
for (;;) {
if (p->k< key) { //move to right thread
if (p->rightTh)
break;
p = p->r;
}
else if (p->k > key) { // move to left thread
if (p->leftTh)
break;
p = p->l;
}
else {
return;
}
}
N *temp = new N();
temp->k = key;
temp->rightTh= temp->leftTh= true;
if (p->k < key) {
temp->r = p->r;
temp->l= p;
p->r = temp;
p->rightTh= false;
}
else {
temp->r = p;
temp->l = p->l;
p->l = temp;
p->leftTh = false;
}
}
void inorder() { //print the tree
N *temp = root, *p;
for (;;) {
p = temp;
temp = temp->r;
if (!p->rightTh) {
while (!temp->leftTh) {
temp = temp->l;
}
}
if (temp == root)
break;
cout<<temp->k<<" ";
}
cout<<endl;
}
};
int main() {
ThreadedBinaryTree tbt;
cout<<"Threaded Binary Tree\n";
tbt.insert(56);
tbt.insert(23);
tbt.insert(89);
tbt.insert(85);
tbt.insert(20);
tbt.insert(30);
tbt.insert(12);
tbt.inorder();
cout<<"\n";
}Output
Threaded Binary Tree 12 20 23 30 56 85 89
4K+ Views
