- SAS - Home
- SAS - Overview
- SAS - Environment
- SAS - User Interface
- SAS - Program Structure
- SAS - Basic Syntax
- SAS - Data Sets
- SAS - Variables
- SAS - Strings
- SAS - Arrays
- SAS - Numeric Formats
- SAS - Operators
- SAS - Loops
- SAS - Decision Making
- SAS - Functions
- SAS - Input Methods
- SAS - Macros
- SAS - Dates & Times
- SAS - Read Raw Data
- SAS - Write Data Sets
- SAS - Concatenate Data Sets
- SAS - Merging Data Sets
- SAS - Subsetting Data Sets
- SAS - Sort Data Sets
- SAS - Format Data Sets
- SAS - SQL
- SAS - Output Delivery System
- SAS - Simulations
- SAS Data Representation
- SAS - Histograms
- SAS - Bar Charts
- SAS - Pie Charts
- SAS - Scatterplots
- SAS - Boxplots
- SAS Basic Statistical Procedure
- SAS - Arithmetic Mean
- SAS - Standard Deviation
- SAS - Frequency Distributions
- SAS - Cross Tabulations
- SAS - T Tests
- SAS - Correlation Analysis
- SAS - Linear Regression
- SAS - Bland-Altman Analysis
- SAS - Chi-Square
- SAS - Fishers Exact Tests
- SAS - Repeated Measure Analysis
- SAS - One-Way Anova
- SAS - Hypothesis Testing
- SAS Useful Resources
- SAS - Quick Guide
- SAS - Useful Resources
- SAS - Questions and Answers
- SAS - Discussion
SAS - Correlation Analysis
Correlation analysis deals with relationships among variables. The correlation coefficient is a measure of linear association between two variables.Values of the correlation coefficient are always between -1 and +1. SAS provides the procedure PROC CORR to find the correlation coefficients between a pair of variables in a dataset.
Syntax
The basic syntax for applying PROC CORR in SAS is −
PROC CORR DATA = dataset options; VAR variable;
Following is the description of the parameters used −
Dataset is the name of the dataset.
Options is the additional option with procedure like plotting a matrix etc.
Variable is the variable name of the dataset used in finding the correlation.
Example
Correlation coefficients between a pair of variables available in a dataset can be obtained by use their names in the VAR statement.In the below example we use the dataset CARS1 and get the result showing the correlation coefficients between horsepower and weight.
PROC SQL;
create table CARS1 as
SELECT invoice, horsepower, length, weight
FROM
SASHELP.CARS
WHERE make in ('Audi','BMW')
;
RUN;
proc corr data = cars1 ;
VAR horsepower weight ;
BY make;
run;
When the above code is executed, we get the following result −

Correlation Between All Variables
Correlation coefficients between all the variables available in a dataset can be obtained by simply applying the procedure with the dataset name.
Example
In the below example we use the dataset CARS1 and get the result showing the correlation coefficients between each pair of the variables.
proc corr data = cars1 ; run;
When the above code is executed, we get the following result −
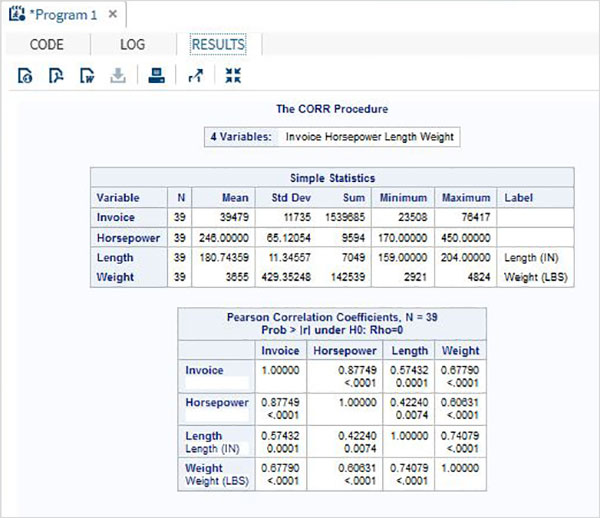
Correlation Matrix
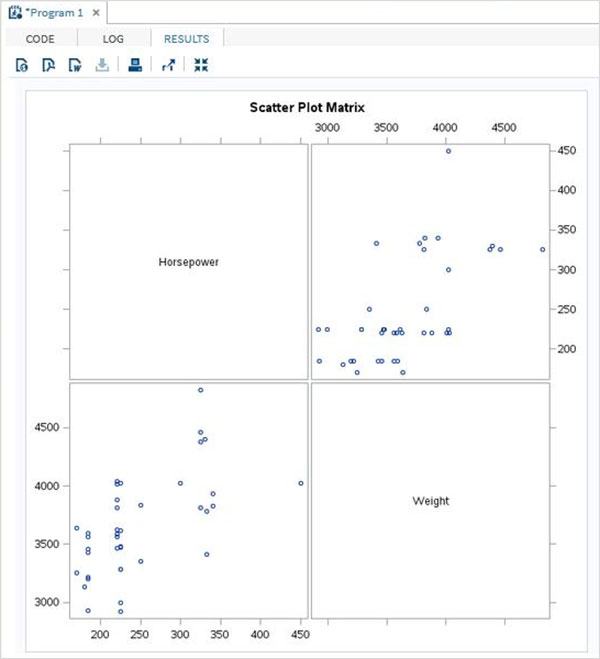
We can obtain a scatterplot matrix between the variables by choosing the option to plot matrix in the PROC statement.
Example
In below example we get the matrix between horsepower and weight.
proc corr data = cars1 plots = matrix ; VAR horsepower weight ; run;
When the above code is executed, we get the following result −