- Radar Systems Tutorial
- Radar Systems - Home
- Radar Systems - Overview
- Radar Systems - Range Equation
- Performance Factors
- Radar Systems - Types of Radars
- Radar Systems - Pulse Radar
- Radar Systems - Doppler Effect
- Radar Systems - CW Radar
- Radar Systems - FMCW Radar
- Radar Systems - MTI Radar
- Delay Line Cancellers
- Radar Systems - Tracking Radar
- Antenna Parameters
- Radar Systems - Radar Antennas
- Matched Filter Receiver
- Radar Systems - Radar Displays
- Radar Systems - Duplexers
- Phased Array Antennas
- Radar Systems Useful Resources
- Radar Systems - Quick Guide
- Radar Systems - Useful Resources
- Radar Systems - Discussion
Radar Systems - Performance Factors
The factors, which affect the performance of Radar are known as Radar performance factors. In this chapter, let us discuss about those factors. We know that the following standard form of Radar range equation, which is useful for calculating the maximum range of Radar for given specifications.
$$R_{Max}=\left [\frac{P_tG\sigma A_e}{\left (4\pi\right )^2 S_{min}}\right ]^{1/4}$$
Where,
$P_t$ is the peak power transmitted by the Radar
$G$ is the gain of transmitting Antenna
$\sigma$ is the Radar cross section of the target
$A_e$ is the effective aperture of the receiving Antenna
$S_{min}$ is the power of minimum detectable signal
From the above equation, we can conclude that the following conditions should be considered in order to get the range of the Radar as maximum.
- Peak power transmitted by the Radar $P_t$ should be high.
- Gain of the transmitting Antenna $G$ should be high.
- Radar cross section of the target $\sigma$ should be high.
- Effective aperture of the receiving Antenna $A_e$ should be high.
- Power of minimum detectable signal $S_{min}$ should be low.
It is difficult to predict the range of the target from the standard form of the Radar range equation. This means, the degree of accuracy that is provided by the Radar range equation about the range of the target is less. Because, the parameters like Radar cross section of the target, $\sigma$ and minimum detectable signal, $S_{min}$ are statistical in nature.
Minimum Detectable Signal
If the echo signal has minimum power, detecting that signal by the Radar is known as minimum detectable signal. This means, Radar cannot detect the echo signal if that signal is having less power than that of minimum power.
In general, Radar receives the echo signal in addition with noise. If the threshold value is used for detecting the presence of the target from the received signal, then that detection is called threshold detection.
We have to select proper threshold value based on the strength of the signal to be detected.
A high threshold value should be chosen when the strength of the signal to be detected is high so that it will eliminate the unwanted noise signal present in it.
Similarly, a low threshold value should be chosen when the strength of the signal to be detected is low.
The following figure illustrates this concept −
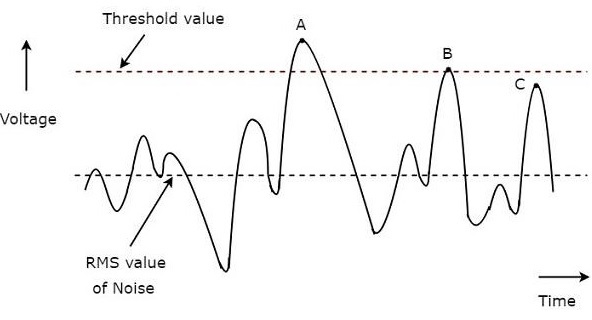
A typical waveform of the Radar receiver is shown in the above figure. The x-axis and y-axis represent time and voltage respectively. The rms value of noise and threshold value are indicated with dotted lines in the above figure.
We have considered three points, A, B & C in above figure for identifying the valid detections and missing detections.
The value of the signal at point A is greater than threshold value. Hence, it is a valid detection.
The value of the signal at point B is equal to threshold value. Hence, it is a valid detection.
Even though the value of the signal at point C is closer to threshold value, it is a missing detection. Because, the value of the signal at point C is less than threshold value.
So, the points, A & B are valid detections. Whereas, the point C is a missing detection.
Receiver Noise
If the receiver generates a noise component into the signal, which is received at the receiver, then that kind of noise is known as receiver noise. The receiver noise is an unwanted component; we should try to eliminate it with some precautions.
However, there exists one kind of noise that is known as the thermal noise. It occurs due to thermal motion of conduction electrons. Mathematically, we can write thermal noise power, $N_i$ produced at receiver as −
$$N_i=KT_oB_n$$
Where,
$K$ is the Boltzmann's constant and it is equal to $1.38\times 10^{-23}J/deg$
$T_o$ is the absolute temperature and it is equal to $290^0K$
$B_n$ is the receiver band width
Figure of Merit
The Figure of Merit, F is nothing but the ratio of input SNR, $(SNR)_i$ and output SNR, $(SNR)_o$. Mathematically, it can be represented as −
$$F=\frac{(SNR)_i}{(SNR)_o}$$
$$\Rightarrow F=\frac{S_i/N_i}{S_o/N_o}$$
$$\Rightarrow F=\frac{N_oS_i}{N_iS_o}$$
$$\Rightarrow S_i=\frac{FN_iS_o}{N_o}$$
Substitute, $N_i=KT_oB_n$ in above equation.
$$\Rightarrow S_i=FKT_oB_n\left ( \frac{S_o}{N_o}\right )$$
Input signal power will be having minimum value, when output SNR is having minimum value.
$$\Rightarrow S_{min}=FKT_oB_n\left ( \frac{S_o}{N_o}\right )_{min}$$
Substitute, the above $S_{min}$ in the following standard form of Radar range equation.
$$R_{Max}=\left [\frac{P_tG\sigma A_e}{\left (4\pi\right )^2 S_{min}}\right ]^{1/4}$$
$$\Rightarrow R_{Max}=\left [\frac{P_tG\sigma A_e}{\left (4\pi\right )^2 FKT_oB_n\left ( \frac{S_o}{N_o}\right )_{min}}\right ]^{1/4}$$
From the above equation, we can conclude that the following conditions should be considered in order to get the range of the Radar as maximum.
- Peak power transmitted by the Radar, $P_t$ should be high.
- Gain of the transmitting Antenna $G$ should be high.
- Radar cross section of the target $\sigma$ should be high.
- Effective aperture of the receiving Antenna $A_e$ should be high.
- Figure of Merit F should be low.
- Receiver bandwidth $B_n$ should be low.