Radar Systems - Matched Filter Receiver

If a filter produces an output in such a way that it maximizes the ratio of output peak power to mean noise power in its frequency response, then that filter is called Matched filter.

This is an important criterion, which is considered while designing any Radar receiver. In this chapter, let us discuss the frequency response function of Matched filter and impulse response of Matched filter.

Frequency Response Function of Matched Filter

The frequency response of the Matched filter will be proportional to the complex conjugate of the input signal’s spectrum. Mathematically, we can write the expression for frequency response function, $H\left (f\right )$ of the Matched filter as −

$$H\left (f\right )=G_aS^\ast\left (f\right )e^{-j2\pi ft_1}\:\:\:\:\:Equation\:1$$

Where,

$G_a$ is the maximum gain of the Matched filter

$S\left (f\right )$ is the Fourier transform of the input signal, $s\left (t\right )$

$S^\ast\left (f\right )$ is the complex conjugate of $S\left (f\right )$

$t_1$ is the time instant at which the signal observed to be maximum

In general, the value of $G_a$ is considered as one. We will get the following equation by substituting $G_a=1$ in Equation 1.

$$H\left (f\right )=S^\ast\left (f\right )e^{-j2\pi ft_1}\:\:\:\:\:Equation\:2$$

The frequency response function, $H\left (f\right )$ of the Matched filter is having the magnitude of $S^\ast\left (f\right )$ and phase angle of $e^{-j2\pi ft_1}$, which varies uniformly with frequency.

Impulse Response of Matched Filter

In time domain, we will get the output, $h(t)$ of Matched filter receiver by applying the inverse Fourier transform of the frequency response function, $H(f)$.

$$h\left (t\right )=\int_{-\infty }^{\infty }H\left (f\right )e^{-j2\pi ft_1}df\:\:\:\:\:Equation\:3$$

Substitute, Equation 1 in Equation 3.

$$h\left (t\right )=\int_{-\infty }^{\infty }\lbrace G_aS^\ast\left (f\right )e^{-j2\pi ft_1}\rbrace e^{j2\pi ft}df$$

$$\Rightarrow h\left (t\right )=\int_{-\infty }^{\infty }G_aS^\ast\left (f\right )e^{-j2\pi f\left (t_1-t\right )}df\:\:\:\:\:Equation\:4$$

We know the following relation.

$$S^\ast\left (f\right )=S\left (-f\right )\:\:\:\:\:Equation\:5$$

Substitute, Equation 5 in Equation 4.

$$h\left (t\right )=\int_{-\infty }^{\infty }G_aS(-f)e^{-j2\pi f\left (t_1-t\right )}df$$

$$\Rightarrow h\left (t\right )=\int_{-\infty }^{\infty }G_aS^\left (f\right )e^{j2\pi f\left (t_1-t\right )}df$$

$$\Rightarrow h\left (t\right )=G_as(t_1−t)\:\:\:\:\:Equation\:6$$

In general, the value of $G_a$ is considered as one. We will get the following equation by substituting $G_a=1$ in Equation 6.

$$h(t)=s\left (t_1-t\right )$$

The above equation proves that the impulse response of Matched filter is the mirror image of the received signal about a time instant $t_1$. The following figures illustrate this concept.

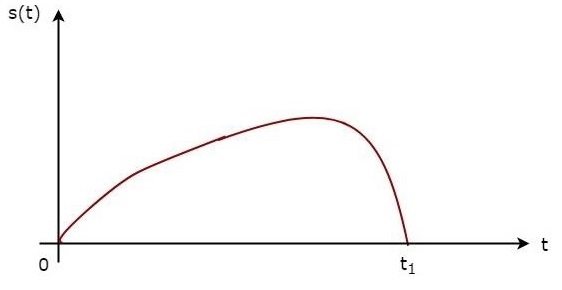
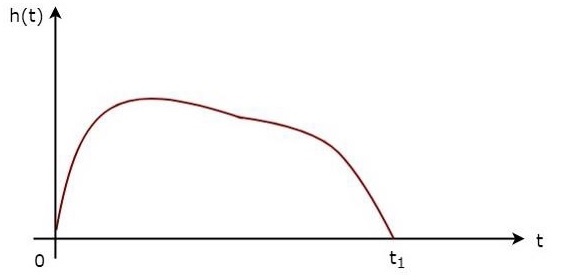
Impulse Response Matched Filter

The received signal, $s\left (t\right )$ and the impulse response, $h\left (t\right )$ of the matched filter corresponding to the signal, $s\left (t\right )$ are shown in the above figures.

Advertisements