Radar Systems - Overview

RADAR is an electromagnetic based detection system that works by radiating electromagnetic waves and then studying the echo or the reflected back waves.

The full form of RADAR is RAdio Detection And Ranging. Detection refers to whether the target is present or not. The target can be stationary or movable, i.e., non-stationary. Ranging refers to the distance between the Radar and the target.

Radars can be used for various applications on ground, on sea and in space. The applications of Radars are listed below.

  • Controlling the Air Traffic
  • Ship safety
  • Sensing the remote places
  • Military applications

In any application of Radar, the basic principle remains the same. Let us now discuss the principle of radar.

Basic Principle of Radar

Radar is used for detecting the objects and finding their location. We can understand the basic principle of Radar from the following figure.

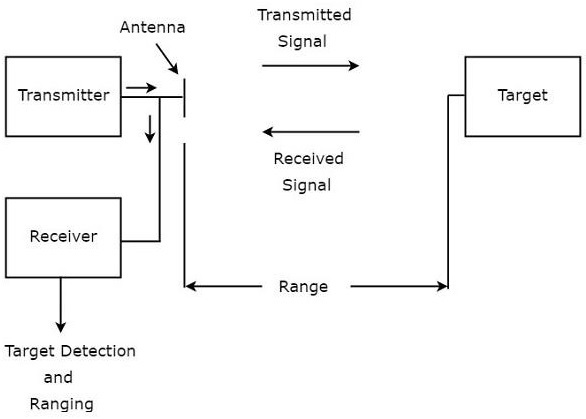
Basic Principal

As shown in the figure, Radar mainly consists of a transmitter and a receiver. It uses the same Antenna for both transmitting and receiving the signals. The function of the transmitter is to transmit the Radar signal in the direction of the target present.

Target reflects this received signal in various directions. The signal, which is reflected back towards the Antenna gets received by the receiver.

Terminology of Radar Systems

Following are the basic terms, which are useful in this tutorial.

  • Range
  • Pulse Repetition Frequency
  • Maximum Unambiguous Range
  • Minimum Range

Now, let us discuss about these basic terms one by one.

Range

The distance between Radar and target is called Range of the target or simply range, R. We know that Radar transmits a signal to the target and accordingly the target sends an echo signal to the Radar with the speed of light, C.

Let the time taken for the signal to travel from Radar to target and back to Radar be ‘T’. The two way distance between the Radar and target will be 2R, since the distance between the Radar and the target is R.

Now, the following is the formula for Speed.

$$Speed= \frac{Distance}{Time}$$

$$\Rightarrow Distance=Speed\times Time$$

$$\Rightarrow 2R=C\times T$$

$$R=\frac{CT}{2}\:\:\:\:\:Equation\:1$$

We can find the range of the target by substituting the values of C & T in Equation 1.

Pulse Repetition Frequency

Radar signals should be transmitted at every clock pulse. The duration between the two clock pulses should be properly chosen in such a way that the echo signal corresponding to present clock pulse should be received before the next clock pulse. A typical Radar wave form is shown in the following figure.

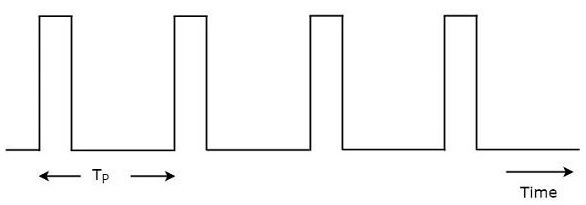
Pulse Repetition Frequency

As shown in the figure, Radar transmits a periodic signal. It is having a series of narrow rectangular shaped pulses. The time interval between the successive clock pulses is called pulse repetition time, $T_P$.

The reciprocal of pulse repetition time is called pulse repetition frequency, $f_P$. Mathematically, it can be represented as

$$f_P=\frac{1}{T_P}\:\:\:\:\:Equation\:2$$

Therefore, pulse repetition frequency is nothing but the frequency at which Radar transmits the signal.

Maximum Unambiguous Range

We know that Radar signals should be transmitted at every clock pulse. If we select a shorter duration between the two clock pulses, then the echo signal corresponding to present clock pulse will be received after the next clock pulse. Due to this, the range of the target seems to be smaller than the actual range.

So, we have to select the duration between the two clock pulses in such a way that the echo signal corresponding to present clock pulse will be received before the next clock pulse starts. Then, we will get the true range of the target and it is also called maximum unambiguous range of the target or simply, maximum unambiguous range.

Substitute, $R=R_{un}$ and $T=T_P$ in Equation 1.

$$R_{un}=\frac{CT_P}{2}\:\:\:\:\:Equation\:3$$

From Equation 2, we will get the pulse repetition time, $T_P$ as the reciprocal of pulse repetition frequency, $f_P$. Mathematically, it can be represented as

$$T_P=\frac{1}{f_P}\:\:\:\:\:Equation\:4$$

Substitute, Equation 4 in Equation 3.

$$R_{un}=\frac{C\left ( \frac{1}{f_P} \right )}{2}$$

$$R_{un}=\frac{C}{2f_P}\:\:\:\:\:Equation\:5$$

We can use either Equation 3 or Equation 5 for calculating maximum unambiguous range of the target.

  • We will get the value of maximum unambiguous range of the target, $R_{un}$ by substituting the values of $C$ and $T_P$ in Equation 3.

  • Similarly, we will get the value of maximum unambiguous range of the target, $R_{un}$ by substituting the values of $C$ and $f_P$ in Equation 5.

Minimum Range

We will get the minimum range of the target, when we consider the time required for the echo signal to receive at Radar after the signal being transmitted from the Radar as pulse width. It is also called the shortest range of the target.

Substitute, $R=R_{min}$ and $T=\tau$ in Equation 1.

$$R_{min}=\frac{C\tau}{2}\:\:\:\:\:Equation\:6$$

We will get the value of minimum range of the target, $R_{min}$ by substituting the values of $C$ and $\tau$ in Equation 6.

Advertisements