Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Program to Connect a Forest in Python
Suppose we have graphs as an adjacency lists. This graph is actually a set of disjoint trees. We have to add a certain number of edges to the forest such that it becomes a single tree. We have to return the minimum distance possible of the longest path between any two nodes. So, if the input is like
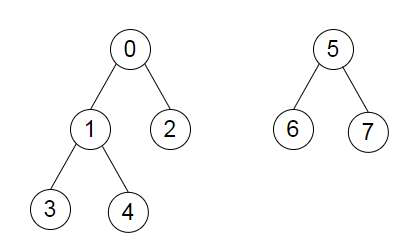
then the output will be 4.
We can add the edge 0 −> 5. Then, the longest path can be any of 3 −> 1 −> 0 −> 5 −> 7 or 4 −> 1 −> 0 −> 5 −> 7; and also these paths with the direction inverted. So we return the distance 4.
To solve this, we will follow these steps −
seen := a new set
dic := graph
Define a function treeDepth(). This will take node.
ret := 0
Define a function dfs1(). This will take node, parent.
add a node in set seen
best2 := an empty min heap structure
for each nxt in dic[node], do
if nxt is not same as parent, then
push(dfs1(nxt, node) + 1) into best2
if len(best2) > 2, then
pop from heap(best2)
if best2 is empty, then
return 0
ret := maximum of ret, sum of all elements of best2
return maximum of best2
dfs1(node, null)
return ret
From the main method do the following −
ret := 0, opt := a new list, sing := 0
for node in range 0 to size of graph, do
if node is present in seen, then
go for next iteration
res := treeDepth(node)
sing := maximum of sing, res
insert the ceiling of (res / 2) at the end of opt
if size of opt <= 1, then
return sing
mx := maximum of opt
for i in range 0 to size of opt, do
if opt[i] is same as mx, then
opt[i] := opt[i] − 1
come out from the loop
for i in range 0 to size of opt, do
opt[i] := opt[i] + 1
high2 := largest 2 elements from opt.
return maximum of sum(high2) and sing
Let us see the following implementation to get better understanding −
Example
import heapq, math class Solution: def solve(self, graph): seen = set() dic = graph def treeDepth(node): self.ret = 0 def dfs1(node, parent): seen.add(node) best2 = [] for nxt in dic[node]: if nxt != parent: heapq.heappush(best2, dfs1(nxt, node) + 1) if len(best2) > 2: heapq.heappop(best2) if not best2: return 0 self.ret = max(self.ret, sum(best2)) return max(best2) dfs1(node, None) return self.ret ret = 0 opt = [] sing = 0 for node in range(len(graph)): if node in seen: continue res = treeDepth(node) sing = max(sing, res) opt.append(int(math.ceil(res / 2))) if len(opt) <= 1: return sing mx = max(opt) for i in range(len(opt)): if opt[i] == mx: opt[i] −= 1 break for i in range(len(opt)): opt[i] += 1 high2 = heapq.nlargest(2, opt) return max(sum(high2), sing) ob = Solution() graph = [ [1, 2], [0,3,4], [0], [1], [1], [6,7], [5], [5] ] print(ob.solve(graph))
Input
graph = [ [1, 2], [0,3,4], [0], [1], [1], [6,7], [5], [5] ]
Output
4
103 Views
To Continue Learning Please Login